Сегодня на уроке мы с вами вспомним формулы, позволяющие перейти от вычисления синуса, косинуса, тангенса и котангенса отрицательных углов к вычислению их значений для положительных углов, а также формулы приведения. Напомним, какие функции называются тригонометрическими. Поговорим о чётности, нечётности тригонометрических функций, а также об их периодичности.
Прежде чем приступить к рассмотрению новой темы, давайте вспомним формулы, которые позволяют сводить вычисление значений синуса, косинуса, тангенса и котангенса отрицательных углов к вычислению их значений для положительных углов.
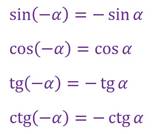
Напомним:
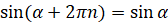 ,
, 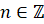 ,
,
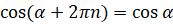 ,
, 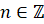 ,
,
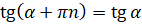 ,
, 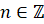 ,
,
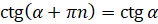 ,
, 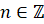 .
.
Вспомним формулы приведения для синуса, косинуса, тангенса и котангенса.
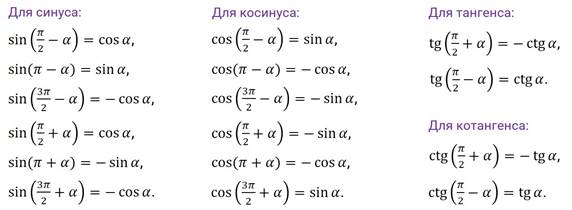
На прошлом занятии мы с вами сказали, что функции  ,
,  ,
,  и
и  называются тригонометрическими функциями.
называются тригонометрическими функциями.
Также на прошлом занятии мы выяснили, что функция  определена на множестве действительных чисел. Для любого значения
определена на множестве действительных чисел. Для любого значения
 верно равенство
верно равенство  . Следовательно, функция
. Следовательно, функция  – нечётная функция.
– нечётная функция.
Функция  определена на множестве действительных чисел. Для любого значения
определена на множестве действительных чисел. Для любого значения
 верно равенство
верно равенство  . Следовательно, функция и
. Следовательно, функция и – чётная функция.
– чётная функция.
Областью определения функции  является множество действительных чисел, кроме
является множество действительных чисел, кроме  ,
, 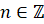 . Для любого
. Для любого  из области определения верно равенство
из области определения верно равенство  . Следовательно, функция
. Следовательно, функция  – нечётная функция.
– нечётная функция.
Областью определения функции  является множество действительных чисел, кроме
является множество действительных чисел, кроме  ,
, 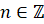 . Для любого
. Для любого  из области определения верно равенство
из области определения верно равенство  . Следовательно, функция
. Следовательно, функция  – нечётная функция.
– нечётная функция.
Отметим, что при исследовании функции на чётность или нечётность мы будем находить её область определения, чтобы убедиться, что эта область определения симметрична относительно начала координат.
Давайте выполним задание. Установите чётность или нечётность функций:
а)  ; б)
; б)  .
.
Решение.
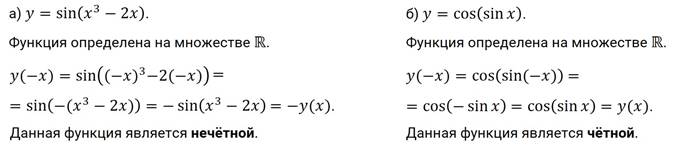
Мы знаем, что для любого значения  верны равенства:
верны равенства:  ,
,  . Из этих равенств следует, что значения синуса и косинуса
периодически повторяются при изменении аргумента на
. Из этих равенств следует, что значения синуса и косинуса
периодически повторяются при изменении аргумента на  . Такие функции называются периодическими с периодом
. Такие функции называются периодическими с периодом  .
.
Функция  называется периодической, если существует такое число
называется периодической, если существует такое число  , что для любого
, что для любого  из области определения этой функции выполняется равенство
из области определения этой функции выполняется равенство
 .
.
Число  называется периодом функции
называется периодом функции  .
.
Из этого определения следует, что если  принадлежит области определения функции
принадлежит области определения функции  , то числа
, то числа  ,
,  и все числа
и все числа  , где
, где 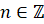 , также принадлежат области определения этой периодической функции
и
, также принадлежат области определения этой периодической функции
и  , где
, где 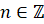 .
.
Число  является наименьшим положительным периодом для функций
является наименьшим положительным периодом для функций  и
и  .
.
Давайте докажем это, например, для функции  .
.
Пусть  – период косинуса, то есть равенство
– период косинуса, то есть равенство  выполняется для любого
выполняется для любого  . При
. При  получаем
получаем  ,
,  . Отсюда
. Отсюда  ,
,  .
.
Так как  , то
, то  может принимать значения
может принимать значения  при
при  ,
,  при
при  ,
,  при
при  и так далее.
и так далее.
Поэтому период не может быть меньше  . То есть
. То есть  – наименьший положительный период функции
– наименьший положительный период функции  .
.
Задание. Докажите, что  – периодическая функция с периодом
– периодическая функция с периодом  .
.
Решение.
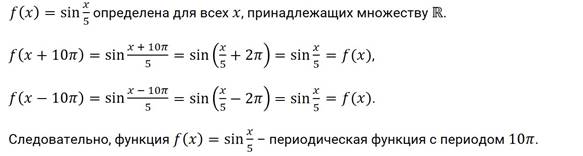
Теперь докажем, что функция  является периодической с наименьшим положительным периодом
является периодической с наименьшим положительным периодом  .
.
Итак, пусть  принадлежит области определения функции
принадлежит области определения функции  , то есть множеству действительных чисел, кроме
, то есть множеству действительных чисел, кроме  ,
, 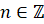 .
.
 ,
,  .
.
Таким образом, мы получили, что  . Следовательно,
. Следовательно,  – период функции
– период функции  .
.
Докажем, что это наименьший положительный период функции  . Пусть
. Пусть  – период тангенса, тогда
– период тангенса, тогда  .
.
При  получаем
получаем  ,
,  . Откуда
. Откуда  ,
,  .
.
При  , то есть при наименьшем целом положительном, получаем
, то есть при наименьшем целом положительном, получаем  . Следовательно,
. Следовательно,  – наименьший положительный период функции
– наименьший положительный период функции  .
.
Отметим, что функция  также является периодической с наименьшим положительным периодом
также является периодической с наименьшим положительным периодом  .
.
Задание. Докажите, что  – периодическая функция с периодом
– периодическая функция с периодом  .
.
Решение.

Задание. Докажите, что  – периодическая функция с периодом
– периодическая функция с периодом  .
.
Решение.

Отметим, что периодическими функциями описываются такие физические процессы, как колебания маятника, вращение планет, переменный ток и так далее.
Сейчас на рисунке вы видите графики некоторых периодических функций. Отметим, что график периодической функции имеет один и тот же вид на всех последовательных отрезках числовой прямой, длина которых равна периоду.

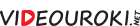
 Получите свидетельство
Получите свидетельство Вход
Вход




 5988
5988

