Посмотрите на гравюру немецкого художника Альбрехта Дюрера, которая была создана в 1514 году.

Если всмотреться в её правый верхний угол, то можно увидеть квадрат размером 4 на 4 клетки.

Этот квадрат является примером того, что математики называют магическим квадратом. А так как он размером 4 на 4, то его называют магическим квадратом четвёртого порядка.
Слово «порядок» означает в данном случае количество клеток на одной стороне квадрата.
Вообще, магические квадраты – это квадраты, разбитые на определённое количество маленьких квадратиков, или клеток, в которые вписаны числа. При этом числа расположены так, что суммы чисел вдоль каждого горизонтального ряда, каждого вертикального столбца, а также каждой из двух диагоналей всегда одинаковы.

А вот если в квадрате равны суммы чисел только в строках и столбцах, то он называется полумагическим.

Сейчас посмотрите на магический квадрат Альбрехта Дюрера, который изображён на гравюре.

Обратите внимание на то, что этот квадрат заполнен числами от 1 до 16.
Если сложить числа в любом горизонтальном ряду этого квадрата, то получится 34.
16 + 3 + 2 + 13 = 34, 5 + 10 + 11 + 8 = 34, 9 + 6 + 7 + 12 = 34, 4 + 15 + 14 +1 = 34
Если сложить числа в каждом вертикальном столбце этого квадрата, то также получится 34.
16 + 5 + 9 + 4 = 34, 3 + 10 + 6 + 15 = 34, 2 + 11 + 7 + 14 = 34, 13 + 8 + 12 + 1 = 34
Сложив числа по диагонали, которая идёт из верхнего правого угла данного квадрата в нижний левый угол, опять получим 34.
4 + 6 + 11 + 13 = 34
Сложив числа по диагонали, которая идёт из верхнего левого угла в нижний правый угол этого квадрата, снова получим 34.
16 + 10 + 7 + 1 = 34
Сумма чисел в каждой строке, столбце и на диагоналях, называется магической константой. Обозначается она большой буквой М.
Магическая константа только что рассмотренного магического квадрата равна 34.
Константа – это постоянная величина. Она не меняется.
И вправду, каждая сумма в нашем примере равна 34, то есть она постоянная, не меняется. Именно поэтому её можно назвать константой.
А чтобы вы не забыли этого слова, я хочу вам рассказать, что имя Костя, Константин в переводе с латинского означает «постоянный».
Магические квадраты были известны китайцам или индийцам уже несколько тысячелетий назад. Встречаются китайские амулеты с магическими квадратами, в которых ещё нет цифр, но есть определённое количество проколов или углублений. Магические квадраты были известны также и арабам в IX веке нашей эры. В Европу магический квадрат проник благодаря некоему греку по имени Москопулос, который жил в Константинополе в начале XV столетия.
Сейчас вы видите изображение, которое считается самым древним магическим квадратом. Говорят, что он впервые появился в Китае примерно за 2800 лет до нашей эры. Под названием Лох-Шу он до сих пор используется как талисман.

Сейчас посмотрите на такой магический квадрат.

Это магический квадрат третьего порядка. Он заполнен числами от 1 до 9.
Сложив числа в любом горизонтальном ряду этого квадрата, получим 15. Сложив числа в любом вертикальном столбце, также получим 15. Сложив числа по диагонали, которая идёт из верхнего правого угла в нижний левый, тоже получаем 15. И сложив числа по диагонали, которая идёт из верхнего левого угла в нижний правый угол этого квадрата, снова 15.

Получается, магическая константа этого квадрата равна 15.
Сейчас вы видите магический квадрат третьего порядка, который заполнен числами от 1 до 9.
Остальные 7 квадратов получаются из него либо перестановкой строк или столбцов, либо путём поворота квадрата.

Отметим, что магических квадратов четвёртого порядка существует 880 вариантов.

Магического квадрата второго порядка не существует. Но посмотрите на один из магических квадратов размером 5 на 5 клеток, который заполнен числами од 1 до 25. Сумма чисел в каждой строке данного квадрата, в каждом его столбце и на диагоналях равна 65.

То есть его магическая константа – 65.
Теперь посмотрите на такой магический квадрат.

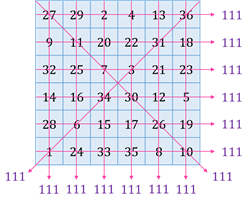
Он шестого порядка, так как количество клеток на одной его стороне равно 6.
Здесь магическая константа равна 111, так как сумма чисел в каждой строке квадрата, в каждом его столбце и на диагоналях равна 111.
Сейчас вы видите квадрат восьмого порядка, который был составлен в XVIII веке Леонардом Эйлером – великим математиком и механиком.
Здесь сумма чисел в каждом вертикальном и горизонтальном ряду равна 260, а сумма чисел половины каждого ряда равна 130.

Отметим, что, сложив каждое число волшебного квадрата с одним и тем же числом или умножив его на одно и то же число, получим новый волшебный квадрат.
Давайте построим магический квадрат размером 3 на 3, у которого расположенное посередине число равно 13.
Возьмём вот такой магический квадрат третьего порядка и попробуем получить другой квадрат, у которого посередине будет число 13.

Поступим следующим образом: вычтем из 13 число, которое расположено посередине данного квадрата, то есть 5.
13 – 5 = 8
Теперь к каждому числу волшебного квадрата прибавим 8.

Выполним сложение в каждой клеточке и получим вот такой новый магический квадрат, у которого посередине расположено число 13.

Построим магический квадрат размером 4 на 4, у которого магическая константа равна 46.
Давайте возьмём, рассмотренный выше магический квадрат Альбрехта Дюрера, у которого константа равна 34, и попробуем получить другой квадрат, у которого магическая константа будет равна 46.

46 – 34 = 12
Магическая константа – это сумма чисел в каждой строке, столбце и на диагоналях. Получается, что константа нового магического квадрата на 12 больше данного.
Так как в каждом ряду и каждом столбце квадрата 4 клетки, то разделив 12 на 4, получим число 3.
12 : 4 = 3
Прибавим 3 к каждому числу волшебного квадрата.

Выполним сложение в каждой клеточке и получим новый магический квадрат, у которого магическая константа равна 46.

Вы можете в этом самостоятельно убедиться. Для этого надо будет найти суммы чисел в каждой строке полученного квадрата, в каждом его столбце, а также на диагоналях.
Ну а сейчас давайте решим задачу. В пустые клетки данного квадрата размером 3 на 3 необходимо вставить числа 4, 6, 9, 10, 11, 12 так, чтобы квадрат стал магическим.

Решение.

Посмотрите на числа, стоящие вдоль одной из диагоналей. Неизвестно только одно число.

Далее посмотрите на числа, которые стоят вдоль другой диагонали. Также неизвестно только одно число.

Найдём число, которое должно стоять в средней клетке верхнего ряда.

Найдём число, которое должно стоять вот в этой клетке.

Затем найдём число, которое должно быть в этой клетке.

И осталось найти ещё одно число.

Вот таким образом, мы вписали данные числа в квадрат так, что он стал магическим.
 Получите свидетельство
Получите свидетельство Вход
Вход




 3329
3329

