Напомним, что частное двух чисел называется отношением этих чисел. Равенство двух отношений называется пропорцией.
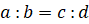 или
или 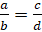 , где
, где 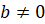 и
и 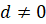 .
.
Числа
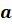 и
и 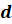 называют крайними
членами пропорции, числа
называют крайними
членами пропорции, числа 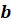 и
и 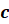 – средними
членами пропорции.
– средними
членами пропорции.
Вспомним свойства пропорции.
1. Произведение крайних членов пропорции равно произведению средних:
если
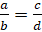 , то
, то 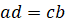 .
.
2.
В пропорции, все члены которой не равны нулю, можно менять местами средние и
крайние члены, то есть если верна пропорция 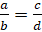 , то верными будут
и пропорции:
, то верными будут
и пропорции:
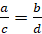 ,
, 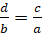 ,
, 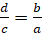 .
.
3.
Если произведение чисел 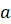 и
и 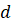 равно
произведению чисел
равно
произведению чисел 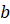 и
и 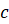 , причём
, причём 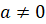 ,
, 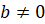 ,
, 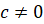 ,
, 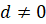 , то из этих чисел
можно составить пропорцию:
, то из этих чисел
можно составить пропорцию:
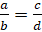 .
.
Переменная
 называется прямо
пропорциональной переменной
называется прямо
пропорциональной переменной  , если
, если  , где
, где  – постоянная и
– постоянная и  .
.
Зависимость,
выраженная формулой  , где
, где  , называется прямой
пропорциональностью, а
, называется прямой
пропорциональностью, а  – коэффициентом
пропорциональности.
– коэффициентом
пропорциональности.
Прямая
пропорциональность переменных означает, что их отношение постоянно, то есть
зависимость между ними при  выражена формулой:
выражена формулой:
 .
.
Пусть
переменные  и
и  прямо
пропорциональны и пусть значениям
прямо
пропорциональны и пусть значениям  и
и  соответствуют
значения
соответствуют
значения  и
и  .
.
Тогда,
если  , для них верно
равенство
, для них верно
равенство  .
.
Переменная
 называется обратно
пропорциональной переменной
называется обратно
пропорциональной переменной  , если
, если  , где
, где  – постоянная и
– постоянная и  .
.
Зависимость,
выраженная формулой  , где
, где  , называется обратной
пропорциональностью, а постоянная
, называется обратной
пропорциональностью, а постоянная  – коэффициентом
обратной пропорциональности.
– коэффициентом
обратной пропорциональности.
Обратная
пропорциональность переменных  и
и  означает, что их
произведение постоянно и не равно нулю, то есть зависимость между ними выражена
формулой:
означает, что их
произведение постоянно и не равно нулю, то есть зависимость между ними выражена
формулой:
 .
.
Пусть
переменные  и
и  обратно
пропорциональные и пусть для значений
обратно
пропорциональные и пусть для значений  и
и  соответствующие
значения равны
соответствующие
значения равны  и
и  .
.
Тогда
для них верно равенство и , или
, или  .
.
Также
напомним, что процентом числа 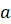 называется его
сотая часть. Следовательно, само число составляет
называется его
сотая часть. Следовательно, само число составляет  .
.
При
решении задач на проценты некоторая величина 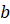 принимается за
принимается за  , а её часть –
величина
, а её часть –
величина 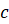 – принимается за
– принимается за  и составляется
пропорция:
и составляется
пропорция:
 .
.
Из
этой пропорции определяют величину  по
правилу нахождения неизвестного члена пропорции:
по
правилу нахождения неизвестного члена пропорции:
 .
.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задание
первое. Найдите  из пропорции
из пропорции  .
.
Решение.

Задание второе. Разделите число 286 на части прямо пропорционально числам 2, 3, 8.
Решение.

Задание третье. Разделите число 286 на части обратно пропорционально числам 1, 2 и 3.
Решение.

Задание
четвёртое. Виноград содержит  воды, а
полученный из него изюм содержит
воды, а
полученный из него изюм содержит  воды. Сколько
изюма получится из
воды. Сколько
изюма получится из  кг винограда?
кг винограда?
Решение.

Задание
пятое. В парке 72 дерева – берёзы и клёны. Берёзы
составляют  всех деревьев.
Сколько берёз надо ещё посадить в парке, чтобы они составляли
всех деревьев.
Сколько берёз надо ещё посадить в парке, чтобы они составляли  всех деревьев?
всех деревьев?
Решение.

Задание шестое. Завод выпускал 852 изделия в месяц. В результате технического перевооружения он стал выпускать 1136 изделий в месяц. На сколько процентов увеличилась производительность завода?
Решение.

Задание
седьмое. В результате увеличения производительности труда на  завод стал
выпускать 920 изделий в месяц. Сколько изделий в месяц выпускал завод ранее?
завод стал
выпускать 920 изделий в месяц. Сколько изделий в месяц выпускал завод ранее?
Решение.

Задание
восьмое. Завод выпускает 500 изделий в год. На сколько
изделий в год увеличится выпуск продукции, если производительность труда
увеличится на  ?
?
Решение.

Задание
девятое. Цену товара сначала повысили на  , а затем понизили
на столько же процентов. На сколько процентов уменьшилась первоначальная цена?
, а затем понизили
на столько же процентов. На сколько процентов уменьшилась первоначальная цена?
Решение.

 Получите свидетельство
Получите свидетельство Вход
Вход





 4834
4834

