Вам
уже знакомы понятия степени числа с натуральным и целым показателями. Напомним,
что степенью с натуральным показателем называется произведение 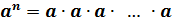 . Здесь
а – основание степени,
. Здесь
а – основание степени,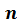 –
показатель степени, при
–
показатель степени, при 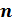
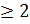 .
.
В
свою очередь, степенью с отрицательным целым показателем
называется 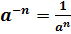 ,
где
,
где 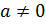 ,
,
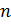 –
натуральное число.
–
натуральное число.
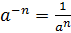 .
.
Однако
в алгебре существует ещё и понятие степени, у которой показатель не целое, а
дробное число. Итак, попытаемся записать 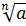 как
некоторую степень числа а, то есть
как
некоторую степень числа а, то есть 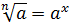 .
.
Мы
знаем, что 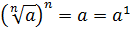 .
Исходя
из того, что мы представили
.
Исходя
из того, что мы представили 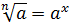 ,
то получим, что
,
то получим, что 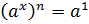 .
По свойству возведения степени в степень имеем
.
По свойству возведения степени в степень имеем 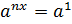 .
Откуда видим, что произведение
.
Откуда видим, что произведение 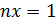 .
Следовательно,
.
Следовательно, 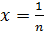 .
.
Тогда
получаем, что 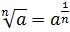 .
По свойству возведения корня n-й
степени в степень получим, что
.
По свойству возведения корня n-й
степени в степень получим, что 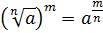 .
.
Например,
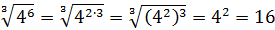
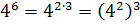
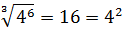
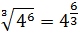
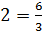 .
.
Сделаем
вывод: если 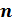 —
натуральное число, причём
—
натуральное число, причём 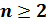 ,
,
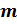 —
целое число и частное
—
целое число и частное  является
целым числом, то при
является
целым числом, то при 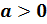 справедливо
равенство
справедливо
равенство 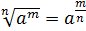 .
.
Пусть
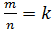 ,
причём
,
причём 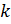 —
целое число. Отсюда
—
целое число. Отсюда 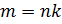 .
Тогда
.
Тогда
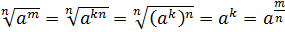 .
.
Если
же частное  не
является целым числом, то степень числа а, где
не
является целым числом, то степень числа а, где 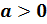 ,
определяют так, чтобы выполнялась формула
,
определяют так, чтобы выполнялась формула 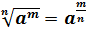 ,
то есть и в этом случае считают, что
,
то есть и в этом случае считают, что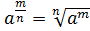 .
.
Таким
образом, формула 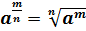 справедлива
для любого целого числа
справедлива
для любого целого числа 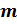 и
любого натурального числа
и
любого натурального числа 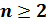 и
положительного основания степени
и
положительного основания степени 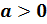 .
.
Например,
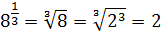
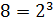
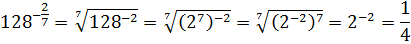
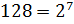 .
.
Напомним,
что рациональное число 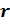 –
это число вида
–
это число вида  ,
где
,
где 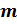 –
целое,
–
целое, 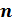 –
натуральное число. Тогда по формуле
–
натуральное число. Тогда по формуле 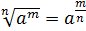 получаем
получаем
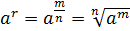 .
.
Таким
образом, степень определена для любого рационального показателя 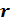 и
любого положительного основания а.
и
любого положительного основания а.
Если
рациональное число 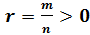 ,
то выражение
,
то выражение 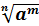 имеет
смысл не только при положительном основании степени, но и при
имеет
смысл не только при положительном основании степени, но и при 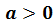 ,
причём
,
причём 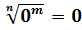 .
Поэтому считают, что
.
Поэтому считают, что 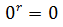 при
при
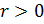 .
.
Пользуясь
формулой 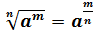 ,
степень с рациональным показателем можно представить в виде корня
и наоборот.
,
степень с рациональным показателем можно представить в виде корня
и наоборот.
Запомните!
Степенью числа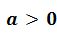 с
рациональным показателем
с
рациональным показателем 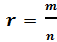 ,
где
,
где 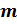 –
целое число, а
–
целое число, а 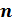 –
натуральное, причём
–
натуральное, причём 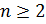 ,
называется число
,
называется число 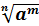 .
.
Замечание:
из определения степени с рациональным показателем
сразу следует, что для любого 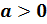 и
любого рационального
и
любого рационального 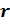 число
число
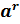 –
положительно.
–
положительно.
Любое
рациональное число допускает различные записи его в виде дроби. По основному
свойству дроби частное  можно
представить, как частное
можно
представить, как частное 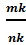 ,
где
,
где
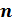 и
и
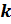 –
натуральные числа,
–
натуральные числа, 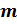 –
целое число. Тогда при любом
–
целое число. Тогда при любом 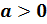 справедливо
равенство
справедливо
равенство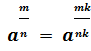 .
.
Что легко доказать применяя свойства корней.
Имеем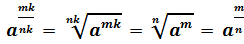 .
.
Заметим, что при отрицательном основании степени рациональная степень числа а не определяется. Отрицательные числа нельзя возводить в рациональную степень, не являющуюся целым числом.
А теперь перейдём к основным свойствам степени и покажем, что все свойства степени с натуральным показателем верны для степени с любым рациональным показателем и положительным основанием.
А
именно для любых рациональных чисел 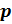 и
и
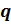 и
любых
и
любых 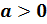 и
и
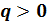 верны
равенства:
верны
равенства:
1.
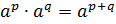 .
.
2.
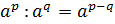 .
.
3.
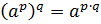 .
.
4.
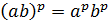 .
.
5.
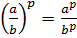 .
.
Для доказательства этих свойств нужно воспользоваться определением степени с рациональным показателем и свойствами корней.
Докажем первое свойство.
1.
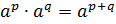 .
.
Итак,
пусть 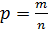 ,
,
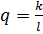 ,
где
,
где 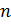 и
и
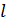 –
натуральные числа,
–
натуральные числа, 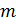 и
и
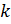 –
целые числа.
–
целые числа.
Нам
нужно доказать, что 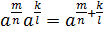 .
.
Приведём
дроби к общему знаменателю 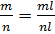 ,
,
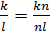 .
.
По определению степени с
рациональным показателем имеем 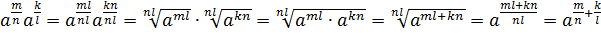 .
.
Аналогичным образом можно доказать и все остальные свойства степени с рациональным показателем.

А теперь давайте приступим к практической части нашего урока.
Задание.
Найдите значения выражения 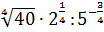 .
.
Решение.
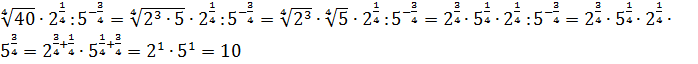 .
.
 Получите свидетельство
Получите свидетельство Вход
Вход




 0
0 8689
8689

