
«Многочлены Чебышёва»
Кряквина Лилия Низамитдиновна,
учитель математики,
МБОУ «Школа № 31»,
г. Ростов-на-Дону

ОГЛАВЛЕНИЕ
- 1. ВВЕДЕНИЕ
- 2. ОСНОВНЫЕ ПОНЯТИЯ
- 3. ГЕОМЕТРИЧЕСКИЙ ПОДХОД
- 4. ЗАКЛЮЧЕНИЕ
- 5. ЛИТЕРАТУРА
- 6. ПРИЛОЖЕНИЯ

ВВЕДЕНИЕ
- Тема исследования работы: многочлены Чебышёва. Объект и предмет исследования: многочлены, наименее уклоняющиеся от нуля на отрезке. Цели и задачи: изучение и анализ свойств приведённых многочленов n-й степени , уклонение которых от нуля наименьшее. Выводы: уклонение от нуля многочленов Чебышёва пропорционально степени длины отрезка, на котором рассматриваются данные многочлены; можно найти итерационный способ построения формул для тригонометрических функций кратных углов. Результаты: построение многочленов, мало уклоняющихся от нуля, на различных отрезках; найден итерационный способ построения формул для тригонометрических функций кратных углов. Новизна темы: проанализированы методы построения бесконечной системы многочленов Чебышёва и их свойства о наименьшем уклонения от нуля на разных интервалах, были найдены многочлены Чебышёва на определённых отрезках, построены графики многочленов четвертой-шестой степени и проведены наблюдения их свойств.

ОСНОВНЫЕ ПОНЯТИЯ
- Многочлены, о которых будет идти речь, встречаются во многих задачах математического анализа, вычислительной математики, алгебры. Они появились в 1854 году в работе русского математика Пафнутия Львовича Чебышёва
- За определение многочленов Чебышёва удобно положить в основу простое рекуррентное соотношение между ними

Рекуррентные соотношения и индукция .
- Положим и . (1) Таким образом могут быть определены многочлены Чебышёва первого рода.
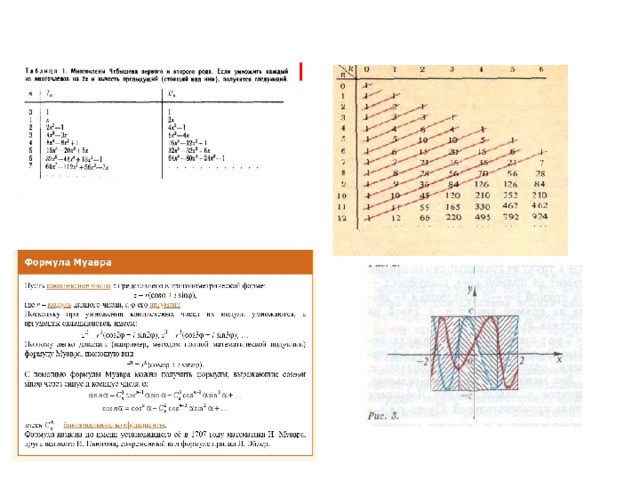
- Выпишем несколько первых членов этой последовательности. Вслед за идут =x*( т.д. (для многочленов до можно проверить результаты по таблице 2 (см. приложение).

С помощью этой таблицы можно построить многочлены Чебышёва до 12 степени

Рассмотрим другой пример: функцию и выразим её через и многочлен от :
;
-1);
. Оказывается, 2 для всех n≥1. (2)
Полученные соотношения нетрудно получить с помощью метода математической индукции и формулы (1). Если предположить, что при k=n-1 и k=n =, то из (1) следует - . Было использовано тождество 2.
Мы провели индуктивный переход не от n к n+1, как обычно, а от n-1и n к n+1; при этом необходимо проверить первые два равенства при n=0 и n=1.

Задача № 1
- Используя соотношения (2), вывести формулу sin5φ=f(sin φ).
- Решение.
- Здесь мы также использовали соотношения (1).
- Итак, не применяя формулу Муавра (см. приложение ), мы получили итерационный способ для построения формул тригонометрических функций кратных углов.

Задача № 2
- Докажите, что а)
- Доказательство.
- Для доказательства используем рекуррентные соотношения (1) и метод математической индукции.
- а) Рассмотрим формулу Если n=1, то Это верно. Допустим, что формула верна при n=k, докажем её справедливость при n=k+1. =2(k+1) - k=2k+2-k=k+2. Итак, Итак, утверждение верно при всех натуральных n.
- б) Рассмотрим Проверим её справедливость при n=1: (-1)(1+1)=-2, т. е. равенство верно. Допустим, что формула верна при n=k, докажем её справедливость при n=k+1. =(k+2). Итак, (k+2). Видим справедливость равенства при всех натуральных n.

ГЕОМЕТРИЧЕСКИЙ ПОДХОД
Геометрический подход.
Задача № 3
Зафиксируем некоторый отрезок числовой оси, например, отрезок . Пусть f(x)= – приведённый многочлен n-й степени (это значит, что его старший коэффициент равен 1). Множество значений f(x) на отрезке – отрезок , где m – минимум, а M – максимум многочлена. Уклонением многочлена от нуля называется наибольшее из чисел Если уклонение многочлена от нуля равно c, то его график содержится в полосе ≤ c и не содержится ни в какой более узкой полосе со средней линией OX. Задача состоит в том, чтобы найти такой приведённый многочлен n-й степени , уклонение которого от нуля было бы минимальным (условие, что старший коэффициент равен 1, не позволяет сжать график произвольно близко к оси абсцисс). Рассмотрим сначала случаи малых степеней. При n=1 речь идёт о линейной функции f(x) = x + a. Её множество значений – отрезок длиной 4. Поэтому наименьшее уклонение от нуля равно 2, а Если n = 2 (случай квадратного трёхчлена), то график многочлена второй степени – отрезок параболы. При этом f(x) = – 2, а уклонение от нуля снова оказывается равным 2.
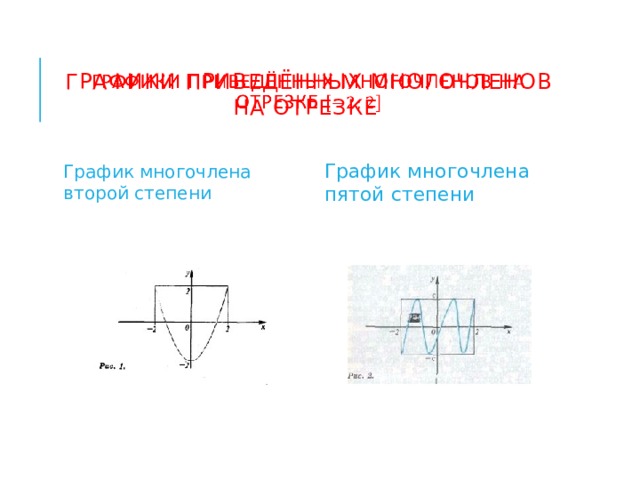
Графики приведённых многочленов на отрезке
График многочлена второй степени
График многочлена пятой степени

Лемма
Функция 2cos nα выражается в виде приведённого многочлена n-й степени от функции 2cosα: 2cosnα = . Например, 2cos2α = 4- 2, т.е. , 2cos3α=8, т.е. .
Лемму можно доказать методом математической индукции.

Задача № 4
Найдите наименьшее уклонение от нуля приведённых многочленов на отрезках: а) ; б) ; в)
Решение
Мы решили задачу на отрезке . Введём линейную замену t=kx+b. Построим многочлены Чебышёва первого рода на нескольких отрезках. При нахождении биномиальных коэффициентов во время построения многочленов Чебышёва используем треугольник Паскаля (см. приложение).
а) x€ . Построим многочлены Чебышёва на отрезке Найдём k и b из условий -2k+b=0, 2k+b=4. Очевидно, что b=2, k=1. t=x+2, x=t-2.
;
; .

б) x€ . Построим многочлены Чебышёва на отрезке
Найдём k и b из условий -2k+b=-1, 2k+b=1. Очевидно, что b=0, k=. t= x, x=2t. Построим многочлены Чебышёва:
в) x€ . Построим многочлены Чебышёва на отрезке
Найдём k и b из условий -2k+b=-4, 2k+b=4..
Итак, =.
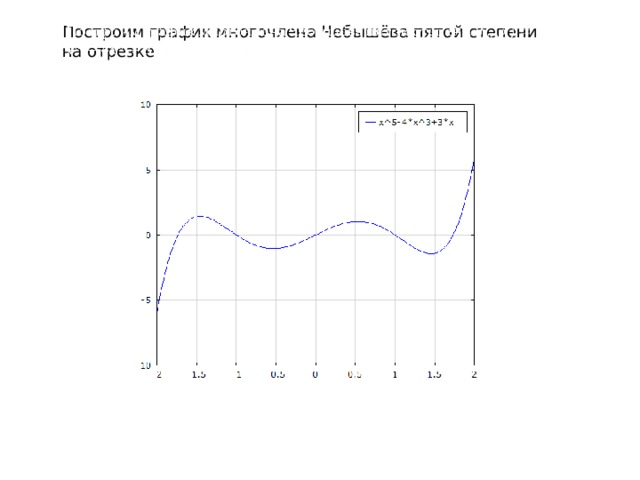
Построим график многочлена Чебышёва пятой степени на отрезке
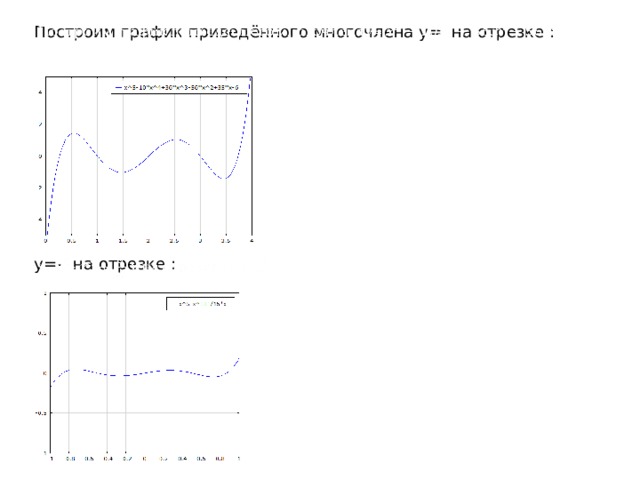
Построим график приведённого многочлена y= на отрезке :
y=- на отрезке :
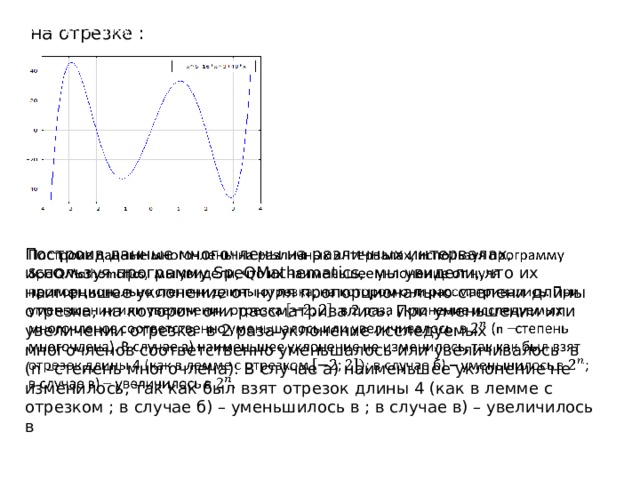
на отрезке :
Построив данные многочлены на различных интервалах, используя программу SpeQMathematics, мы увидели, что их наименьшее уклонение от нуля пропорционально степени длины отрезка, на котором они рассматривались. При уменьшении или увеличении отрезка в 2 раза уклонение исследуемых многочленов соответственно уменьшалось или увеличивалось в (n –степень многочлена). В случае а) наименьшее уклонение не изменилось, так как был взят отрезок длины 4 (как в лемме с отрезком ; в случае б) – уменьшилось в ; в случае в) – увеличилось в
ЗАКЛЮЧЕНИЕ
Представленный в работе материал интересен, актуален и полезен для практического применения, поскольку знакомит с некоторыми методами построения многочленов, мало отклоняющихся от нуля, на отрезке. При решении этой задачи Чебышёва использован геометрический подход и подход, основанный на изучении тригонометрических многочленов. В результате доказано несколько полезных формул, связанных с рекуррентными соотношениями, задающими многочлены Чебышёва; проанализированы методы построения бесконечной системы многочленов Чебышёва первого рода и их свойства о наименьшем уклонении от нуля на разных интервалах; построены графики при n=4,5,6, а также найден итерационный способ построения формул для тригонометрических функций кратных углов. При анализе использовались рекуррентные соотношения и метод математической индукции. Результаты этой исследовательской работы полезны, так как тема остаётся актуальной при решении некоторых задач математического анализа, комбинаторики, вычислительной математики, алгебры. Естественно, что любая удобная для практического использования формула или подход даёт хороший опыт работы с заданиями творческого характера и это интересно.

ЛИТЕРАТУРА
1.Н.Б. Васильев, А.В. Зелевинский. Многочлены Чебышёва и рекуррентные соотношения. Научно-популярный физико-математический журнал «Квант»,1 выпуск-М.: МЦНМО, 1982. – 12-19 с.
2.Н.Б. Васильев. Многочлены Чебышёва. Приложения к Научно-популярному физико-математическому журналу «Квант»,2 выпуск-М.: МЦНМО, 2013. – 18-30 с.
3.С.В. Гашков. Задача Чебышёва и тригонометрические многочлен. Научно-популярный физико-математический журнал «Квант», 6 выпуск-М.: МЦНМО, 1990. – 25-27 с.
4.Д. Пойа, Г. Сеге. Задачи и теоремы из анализа. -М.: Наука, 1978, 84 с.
5.С.Л. Табачников Многочлены, наименее уклоняющееся от нуля. Научно-популярный физико-математический журнал «Квант», 6 выпуск-М.: МЦНМО, 1990. – 23-25 с.
6.А.М. Яглом, И.М. Яглом. Неэлементарные задачи в элементарном изложении. Библиотека математического кружка, 5 выпуск. – М.: Гостехтеориздат,1954. – 130-134 с.
7.https://ru.wikipedia.org/wiki/%D0%9C%D0%BD%D0%BE%D0%B3%D0%BE%D1%87%D0%BB%D0%B5%D0%BD%D1%8B_%D0%A7%D0%B5%D0%B1%D1%8B%D1%88%D1%91%D0%B2%D0%B0?fbclid=IwAR0qNVHR95prFMeJcwmKqaXkNuuTXOuwE15h-VQ0mA4ORdlzkU9Llx-1XhI
ПРИЛОЖЕНИЯ

 Получите свидетельство
Получите свидетельство Вход
Вход












 Многочлены Чебышёва (1.5 MB)
Многочлены Чебышёва (1.5 MB)
 0
0 180
180 5
5 Нравится
0
Нравится
0


