Метод областей.
Для успешного исследования на плоскости многих задач с параметрами может быть использован метод областей – полезный приём, в некотором смысле обобщающий известный метод интервалов. Поясним его на примерах.
Пример №1. Укажите множество точек плоскости (х;у), удовлетворяющих неравенству (х – у)·(х2 – у – 4) ≥ 0.
Решение: обозначим левую часть неравенства через f(х;у), т.е.
f(х;у) = (х – у)·(х2 – у – 4).
1 шаг. f(х;у) определено при любых х R и любых значениях у R.
2 шаг. Найдём множества точек координатной плоскости, для которых f(х;у) обращается в нуль
(х – у)·(х2 – у – 4) = 0
х – у = 0 или х2 – у – 4 = 0
у = х у = х2 – 4
Первое из уравнений определяет прямую, второе параболу. Построим графики этих уравнений в прямоугольной системе координат.
Прямая и парабола разбивают всю плоскость на пять областей, в каждой из которых f(х;у) сохраняет постоянный знак, поэтому для определения
Рисунок 1
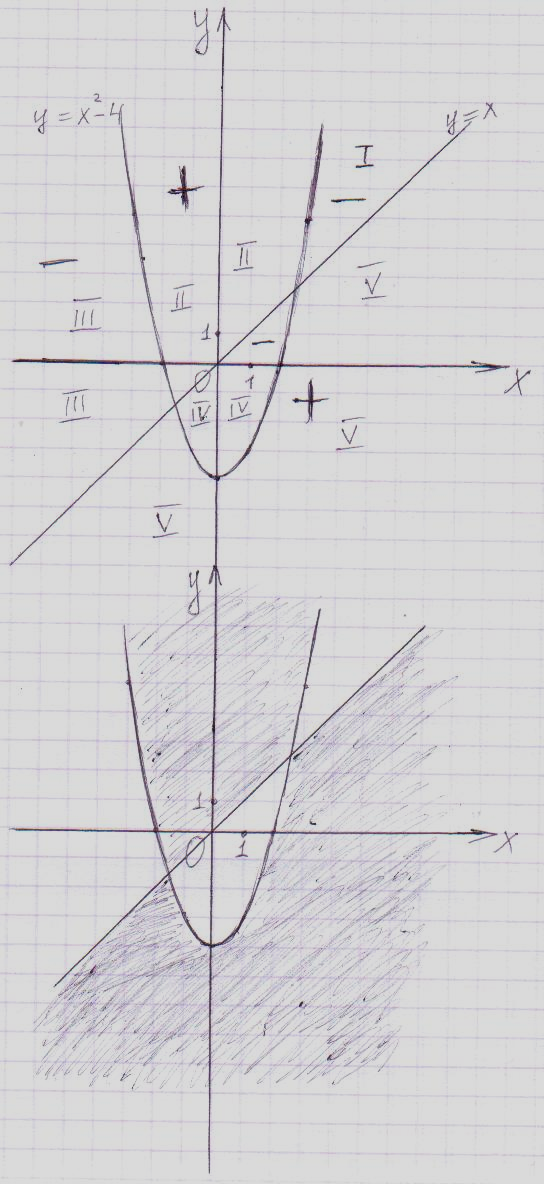
Знака f(х;у) в какой-либо области достаточно знак этой функции в какой-нибудь (любой) точке из этой области. Например из области II возьмём точку с координатами (0;3) и подставим в выражение:
f(0;3) = (0-3)(0-3-4) = -3·(-7) = 210
следовательно, исходное выражение во всех точках области II будет положительно. Аналогичным образом определяются знаки функции f(х;у) во всех остальных областях.
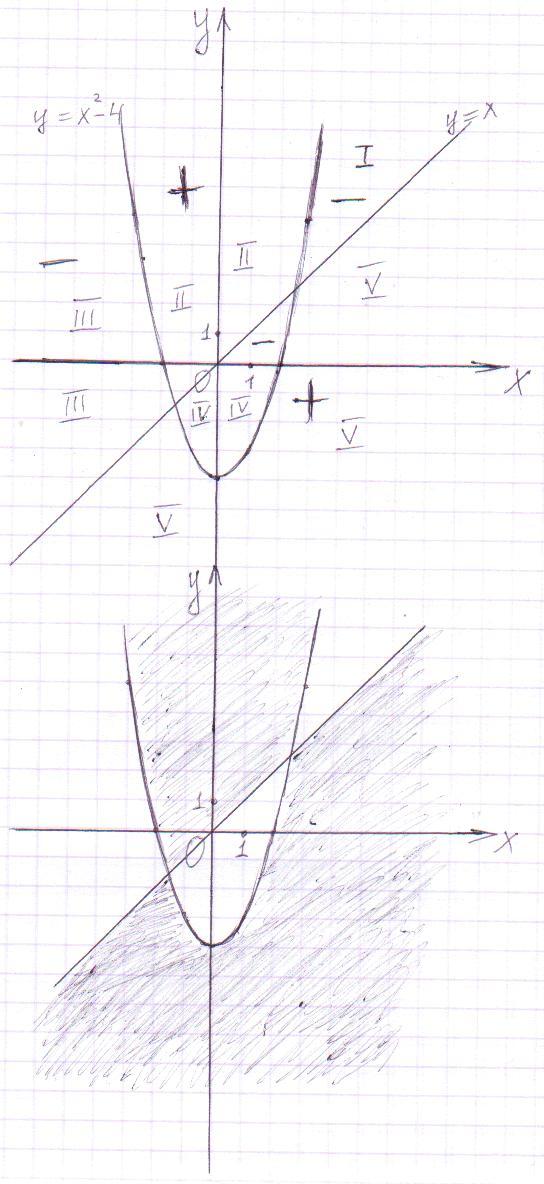
Ответом является множество точек представленных на рисунке 2.
Рисунок 2
Пример №2. Найдите все значения а, при каждом из которых система имеет хотя бы одно решение.
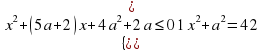
Изобразим множество решений неравенства 1) в системе координат хоа, используем метод областей:
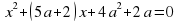
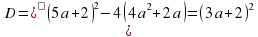
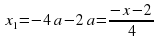
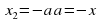
Прямые 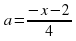 и
и 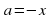 разбивают координатную плоскость на 4 области, в каждой из которых определяет знак квадратного трёхчлена: f(х;а) = х2 + (5а + 2)х + 4а2 + 2а.
разбивают координатную плоскость на 4 области, в каждой из которых определяет знак квадратного трёхчлена: f(х;а) = х2 + (5а + 2)х + 4а2 + 2а.
Рисунок №3

Области, являющиеся решением первого неравенства отмечены штриховкой.
Второе уравнение системы (2) определяет окружность, центр которой находится в начале координат и радиусом 2. Решениями системы на плоскости (х;а) являются дуги этой окружности, проходящие по заштрихованным областям.
Найдём координаты точек пересечения окружности с прямыми.
а) 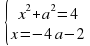 б)
б) 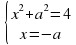
(4а+2)2 + а2 = 4 а2 + а2 = 4
17а2 + 16а = 0 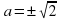
а = 0; а = 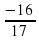 (абсциссы точек пересечения можно не находить).
(абсциссы точек пересечения можно не находить).
Итак, система имеет решения при а 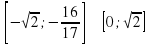
Пример №3. Найдите все значения а, для каждого из которых неравенство
ах2 – 4х + 3а + 1 0 выполняется для любого х [ - 2; 0].
Решение.
Изобразим множество решений неравенства в системе координат хоа, используем метод областей:
ах2 – 4х + 3а + 1 = 0 выразим а через х.
а(х2 + 3) = 4х – 1; 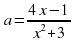 построим график этой функции, используем производную.
построим график этой функции, используем производную.
а) если х →±∞, то а →0.
б) х = 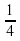 – нуль функции.
– нуль функции.
в) а =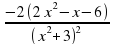
2х2 – х – 6 = 0
Х1 = -3/2
Х2 = 2
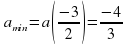
Рисунок №4
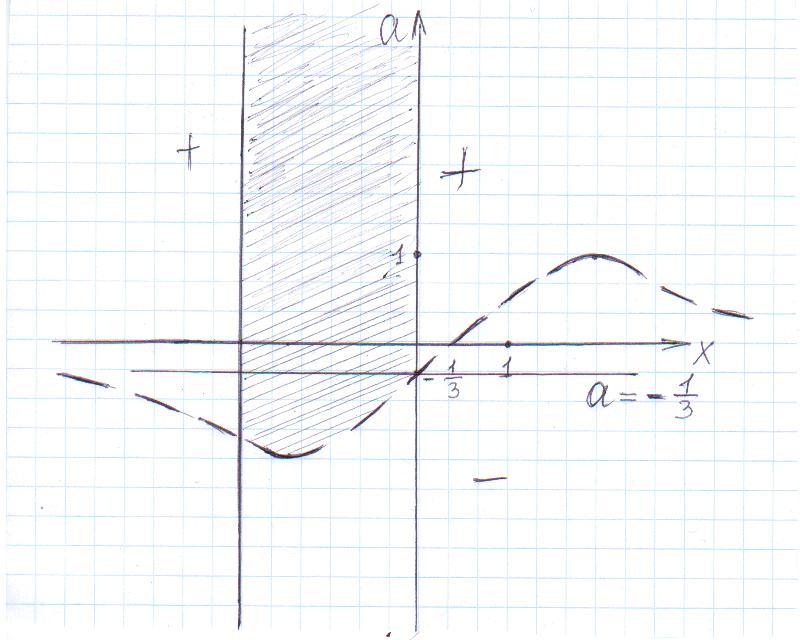
Эта кривая разбивает плоскость на две области, в каждой из которых определяем знак функции f(x;a)=ах2 – 4х + 3а + 1, f(0;0) = 1 0.
Множество точек, удовлетворяющих условию х [-2;0] на координатной плоскости (ха) представляет множество точек, расположенных между прямыми х = -2 и х = а.
Из рисунка видно, что неравенство ах2 – 4х + 3а + 10 будет выполняться при х [-2;0], если а 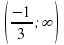
Х = 0
0 – 0 + 3а +1 0; 3а -1; а - 1/3
Ответ: при а 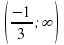 .
.
Пример №4. Для каждого b [ - 3;2] найдите наименьшее значение величины х2, где х – решение неравенства 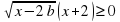 .
.
Решение: введём f(x;b) = 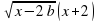
ОДЗ: x – 2b ≥ 0
b ≤ 1/2х
Нули: 
b = x/2 или x = - 2
На координатной плоскости (х;b) отметим штриховкой решения неравенства, применяя метод областей.
Если х = - 2, то b = - 1.
f (0;-2) = 
f (-3;-5) =
Рисунок №5
Отсюда получаем ответ:
Пример №5. При каждом значение параметра решите неравенство:
Решение: введём функцию
ОДЗ:
Найдём нули:
X1=1; x2=3
На координатной плоскости (х;а) проведём прямые х=1; х=3 (с учётом ОДЗ) и определим знак f(x;a) в каждой из полученных областей.
Рисунок №6



На координатной плоскости (х;а) отмечаем штриховкой решения неравенства и исходя из этого записываем ответ:
Если a x [1;3]
Если 0 ≤ a x [1; 2 - а) U (а + 2;3]
Если а = 1, то решений нет
Если 1 a x (2 – а; 1] U [3; а + 2)
Если a ≥ 5/4, то x (3/4; 1] U [3; а + 2)
Литература
О.Ю.Черкасов, А.Г.Якушев. Математика. Интенсивный курс подготовки к экзамену. Айрис Рольф, Москва, 1997г.
Олимпиадные задачи. МИФИ. Под редакцией О.В.Нагорного, Москва 2010.

 Получите свидетельство
Получите свидетельство Вход
Вход





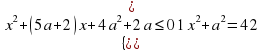
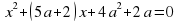
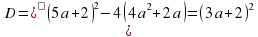
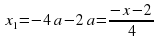
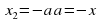
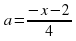 и
и 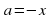 разбивают координатную плоскость на 4 области, в каждой из которых определяет знак квадратного трёхчлена: f(х;а) = х2 + (5а + 2)х + 4а2 + 2а.
разбивают координатную плоскость на 4 области, в каждой из которых определяет знак квадратного трёхчлена: f(х;а) = х2 + (5а + 2)х + 4а2 + 2а.
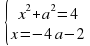 б)
б) 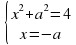
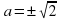
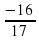 (абсциссы точек пересечения можно не находить).
(абсциссы точек пересечения можно не находить).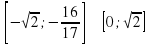
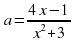 построим график этой функции, используем производную.
построим график этой функции, используем производную.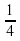 – нуль функции.
– нуль функции.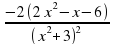
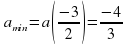
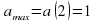

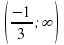
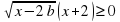 .
.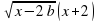









 Практикум по математике "Метод областей" (0.38 MB)
Практикум по математике "Метод областей" (0.38 MB)
 0
0 723
723 57
57 Нравится
0
Нравится
0



