Формулы сокращённого умножения

Вопросы занятия:

·  вспомнить, что называют многочленом;

·  вспомнить, как многочлены приводить к стандартному виду;

·  поговорить о том, как назвать степень многочлена;

· вспомнить, какие действия можно выполнять над многочленами;

· вспомнить, какие существуют способы разложения многочлена на множители.

Материал урока

Формулы сокращённого умножения крайне необходимы во всех разделах математики. Они применяются в умножении многочленов, разложении многочленов на множители, приведении многочленов к стандартному виду, упрощении выражений, решении уравнений, сокращении дробей и т.д.

Формулы сокращённого умножения доказываются непосредственным раскрытием скобок и приведением подобных слагаемых. Эти формулы нужно знать наизусть.

Давайте разберёмся откуда они берутся и как применять.

Итак, перейдём к первому вопросу: откуда берутся формулы сокращённого умножения?

И для начала назовём семь основных формул сокращённого умножения. Итак, это:

Перечисленные равенства верны для любых значений a и b, следовательно, они являются тождествами.

Обратите внимание, равенства третье, шестое и седьмое записаны не очень привычно. Как бы наоборот. Это специально! Ведь нужно помнить, что любое равенство работает как слева направо, так и справа налево.

В такой записи понятнее, откуда берутся формулы сокращённого умножения. Ведь они берутся из умножения!

Перейдём к доказательству этих формул. И первой докажем формулу квадрата суммы.

Доказывать будем её слева направо.

Итак, возведём в квадрат сумму . Для этого представим это выражение в виде произведения двух одинаковых многочленов:  и . Затем выполним умножение этих многочленов, т.е. умножим каждый член первого многочлена на каждый член второго многочлена. Приведём подобные слагаемые. И получим,

Вот и всё, никаких научных хитростей. Просто раскрываем скобки по всем правилам умножения многочленов и приводим подобные.

Так получаются все формулы сокращённого умножения. А называется умножение сокращённым – это потому, что в самих формулах нет промежуточных вычислений (раскрытия скобок и приведения подобных). Сразу дан результат.

Напомним, что читают формулу квадрата суммы так: квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения.

А теперь давайте докажем эту формулу в обратную сторону. Для этого удвоенное произведение  распишем как сумму . Затем сгруппируем первое слагаемое со вторым и третье с четвертым. Обратите внимание, в первой группе можем вынести за скобки общий множитель а, а во второй — b. Теперь видим, что каждое слагаемое имеет общий множитель . Вынесем его за скобки и получим,

Формулу квадрата суммы двух положительных чисел a и b можно изобразить геометрически.

Рассмотрим квадрат.

Если сторона этого квадрата равна сумме , то понятно, что его площадь будет равна:

В двух углах рассматриваемого квадрата построим квадраты со сторонами a и b. Площади полученных квадратов равны соответственно  и .

Большой начальный квадрат, разделён на четыре части: два квадрата с площадями  и  соответственно и два прямоугольника, каждый площадью .

Понятно, что площадь всего начального квадрата равна сумме площадей каждой его части. А значит, площадь квадрата равна:

А ведь это и есть формула квадрата суммы.

Пример. Раскроем скобки в выражении , пользуясь формулой квадрата суммы.

По формуле квадрата суммы имеем:

Затем выполним действия и получим:

Формула квадрата разности доказывается аналогично.

Докажем её. Возведём в квадрат разность . Для этого представим это выражение в виде произведения двух одинаковых многочленов:  и . Затем выполним умножение многочленов. Приведём подобные слагаемые. И получим,

Напомним, что читают формулу квадрата разности так: квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения.

А теперь давайте докажем формулу квадрата разности в обратную сторону. Для этого  распишем как сумму . Затем сгруппируем первое слагаемое со вторым и третье с четвёртым. Обратите внимание, в первой группе можем вынести за скобки общий множитель а, а во второй. Теперь видим, что каждое слагаемое имеет общий множитель . Вынесем его за скобки и получим,

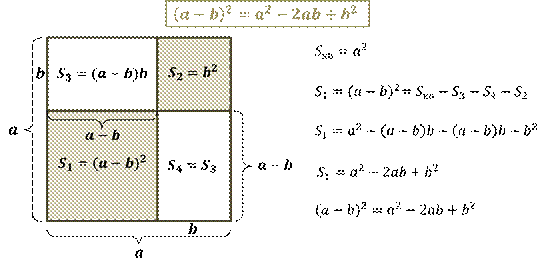
На экране вы видите геометрическую иллюстрацию формулы квадрата разности:

Пример. Раскроем скобки в выражении , пользуясь формулой квадрата разности.

По формуле квадрата разности имеем:

Затем выполним действия и получим,

Следующей докажем формулу разности квадратов двух выражений.

Давайте выполним умножение разности  на сумму .

Воспользуемся правилом умножения многочлена на многочлен. Приведём подобные слагаемые и получим,

Это тождество позволяет сокращённо выполнять умножение разности двух выражений на их сумму.

Читают его так: произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

Теперь докажем формулу разности квадратов в обратную сторону. Для этого к выражению  прибавим 0 (нуль). Напомним, что мы это можем сделать, так как при прибавлении нуля значение выражения не меняется. Затем представим нуль как разность двух одночленов: (). Сгруппируем первое слагаемое со вторым, третье с четвертым. Заметим, что в первой группе можем вынести за скобки общий множитель а, во второй – общий множитель . Теперь видим, что каждое слагаемое имеет общий множитель . Вынесем его за скобки и получим,

Рассмотрим примеры.

а) выполнить умножение: (𝑎−10)(𝑎+10);

б) разложить на множители многочлен: .

В первом примере нужно выполнить умножение. Воспользуемся формулой разности квадратов. Затем возведём в квадрат. Получим,

Во втором примере разложим на множители многочлен: . Заметим, что этот многочлен можно представить, как разность квадратов . Применим формулу разности квадратов. Получим,

Перейдём к следующей формуле. И сейчас мы приведём доказательство формулы куба суммы.

Итак,  можем записать, как . Далее возведём в квадрат сумму во вторых скобках, выполним умножение многочлена на многочлен, приведём подобные слагаемые и получим,

Это тождество и называют формулой куба суммы.

Читают её так: куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго плюс куб второго выражения.

Аналогично доказывается формула куба разности.

Для этого куб разности  представляют в виде произведения . Затем возводят в квадрат разность , выполняют умножение многочленов, приводят подобные слагаемые и получают,

А читают эту формулу так: куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго минус куб второго выражения.

Рассмотрим примеры. Нужно раскрыть скобки, пользуясь формулами куба суммы или куба разности:

а) ;

б) .

Первое выражение . Здесь мы применим формулу куба суммы. И выполнив действия, получим,

Второе выражение . В этом примере раскроем скобки, воспользовавшись формулой куба разности. Затем, выполнив действия, получим,

Для разложения на множители суммы кубов используется одна из формул сокращённого умножения, которая называется формулой суммы кубов.

Чтобы доказать эту формулу мы умножим двучлен  на трёхчлен . Приведём подобные слагаемые и получим,

Обратите внимание, что один из множителей в правой части формулы напоминает нам трёхчлен, равный квадрату разности a и b. Но вместо удвоенного произведения в нём стоит просто произведение a и b. А поэтому трёхчлен  называют неполным квадратом разности a и b.

Читают формулу суммы кубов так: сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

Для разложения на множители разности кубов используется следующая формула сокращённого умножения, которая называется формулой разности кубов.

Для доказательства этой формулы мы умножим двучлен  на трёхчлен . Приведём подобные слагаемые и в результате получим,

В этой формуле множитель  называют неполным квадратом суммы, так как он напоминает трёхчлен, который равен квадрату суммы a и b.

Читают формулу разности кубов следующим образом: разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

Рассмотрим примеры.

Надо разложить многочлены на множители

а) ;

б) .

Первый многочлен . Здесь число 64 можно записать как 4 в кубе. А тогда по формуле разности кубов имеем следующее произведение. Далее выполним действия во вторых скобках и получим,

Второй многочлен . Обратите внимание, первое слагаемое можно представить как , а второе – как . Теперь применим формулу суммы кубов. Затем приведём трёхчлен во вторых скобках к стандартному виду и получим произведение двух множителей:

А теперь давайте рассмотрим, как применять все эти формулы.

Задание.

Найти значение выражения, применяя формулы квадрата суммы и квадрата разности:

а) ;

б) .

Первое выражение: . Представим число 107 в виде суммы чисел 100 и 7. Далее разложим выражение по формуле квадрата суммы. Выполним действия. И в результате получим,

Второе выражение: . Представим число 999 в виде разности чисел 1000 и 1. Раскроем скобки, воспользовавшись формулой квадрата разности. Затем выполним действия. И в результате получим,

Задание.

Представить многочлен в стандартном виде:

.

Заметим, что относительно выражений  и  в условии записана формула квадрата разности. Свернём это выражение. Преобразуем выражение внутри скобок. Возведём в квадрат. И в результате получим,

Задание.

Доказать тождество:

.

Преобразуем левую часть данного равенства. Первые скобки раскроем по формуле куба суммы, а вторые и третьи – по формулам квадрата разности и квадрата суммы двух выражений, соответственно. Затем раскроем скобки, применяя распределительный закон умножения. Приведём подобные. И в результате получим,

Т.е. мы получили правую часть нашего тождества. А значит, доказали его.

Задание.

Сократить дробь:

.

Знаменатель дроби пока оставим прежним. В числителе дроби первое слагаемое представим как , а второе – как . Приведём второй множитель в числителе к стандартному виду. Видим, что неполный квадрат суммы в числителе и выражение в знаменателе можно сократить. А тогда в результате получим,

Задание.

Решить уравнение:

.

В первую очередь упростим левую часть уравнения. К произведению выражений  применим формулу разности кубов. Затем раскроем последние скобки, применяя распределительный закон умножения. Выполним действия. Приведём подобные слагаемые. Тогда получим,

Итоги урока

На этом уроке мы вспомнили формулы сокращённого умножения. Доказали эти формулы. А затем рассмотрели применение их на практике.