Материал урока.
На прошлых уроках вы познакомились с понятием прямой перпендикулярной к плоскости.
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Но, так как плоскость содержит бесконечно много прямых, становится невозможным проверить перпендикулярность данной прямой ко всем прямым плоскости. И вообще, возникают сомнения в том, что такая прямая есть.
Но мы с вами приводили примеры прямых перпендикулярных к плоскости из жизни.
Очевидно, есть способ построения таких прямых. В этом помогает признак перпендикулярности прямой и плоскости.
И звучит он так: если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
Докажем это утверждение.
Но перед этим вспомним свойство, которое активно будем применять при доказательстве. А именно свойство серединного перпендикуляра к отрезку.
Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.

Ну, а каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
Итак, рассмотрим плоскость α; прямые p и q, лежащие в ней и пересекающиеся в точке О; а также прямую a, перпендикулярную к прямым p и q.
Нужно доказать, что прямая a перпендикулярна к плоскости α. То есть перпендикулярна к произвольной прямой m плоскости α.
Рассмотрим случай, когда прямая a проходит через точку О. И через точку О проведём прямую l параллельную прямой m.
Далее отметим на прямой a точки А и B так, чтобы точка О являлась серединой отрезка АB, и проведём в плоскости α прямую пересекающую прямые p, q и l в точках P, Q и L соответственно.
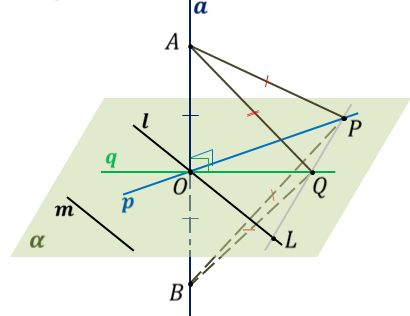
Так как прямая a перпендикулярна к прямым p и q и точка О является серединой отрезка АB, то можно сказать, что прямые p и q являются серединными перпендикулярами к отрезку АB.
Тогда, точка P равноудалена от концов отрезка АB, то есть равны отрезки AP и BP. Аналогично, точка Q равноудалена от концов отрезка АB, и равны отрезки AQ и BQ.
Тогда треугольники APQ и BPQ равны по трём сторонам. Отсюда равны углы APQ и BPQ.

Теперь рассмотрим треугольники APL и BPL. Они равны по двум сторонам и углу между ними.
Тогда равны отрезки AL и BL. Это означает, что точка L равноудалена от концов отрезка AB, а прямая l является серединным перпендикуляром к отрезку АB.
Тем самым мы получили, что прямая l перпендикулярна к прямой a.
Так как прямая m параллельна прямой l, а прямая l перпендикулярна к прямой a, то по лемме о двух параллельных прямых перпендикулярных к третьей получаем, что прямая m так же перпендикулярна к прямой a.
Мы доказали теорему для случая, когда прямая a проходит через точку О. А теперь рассмотрим случай, когда прямая a не проходит через точку О.
Проведём через точку О прямую a1 параллельную прямой a.

Так как прямые a1 и a параллельны, а прямая a перпендикулярна к прямым p и q, то и прямая a1 перпендикулярна к данным прямым. А значит, по первой части доказательства, прямая a1 перпендикулярна к плоскости α.
Но ведь прямая a параллельна прямой a1. Тогда и прямая a перпендикулярна к плоскости α.
Что и требовалось доказать.
На примере прямоугольного параллелепипеда, например, не трудно доказать, что ребро АА1 перпендикулярно к плоскости ABCD.

Действительно, гранями прямоугольного параллелепипеда являются прямоугольники. И можно отметить, что ребро АА1 будет перпендикулярно к ребру АБ, а также перпендикулярно к ребру АД.
Рёбра АБ и АД, в свою очередь, пересекаются в точке А и лежат в плоскости АБЦД. Это означает, что, по признаку перпендикулярности прямой и плоскости, ребро АА1 перпендикулярно к плоскости АБЦД.
Воспользуемся доказанным признаком и решим следующую задачу.
Задача. Доказать, что через любую точку пространства проходит плоскость, перпендикулярная к данной прямой.
Решение.

Если точка M лежит на прямой a, то, аналогично предыдущему доказательству, через прямую a проводят две плоскости и в них проводят перпендикуляры к прямой a через точку M. Плоскость, проходящая через две проведённые прямые, и является искомой.

Стоит заметить, что плоскость γ будет единственной плоскостью проходящей через точку M и перпендикулярной к прямой a.
Посмотрим, как можно применять полученные на этом уроке знания при решении задач.
Задача.
 тетраэдр,
где точка
тетраэдр,
где точка  —
середина ребра
—
середина ребра  .
.
 ,
,
 .
.
Доказать,
что плоскость треугольника  перпендикулярна
к прямой
перпендикулярна
к прямой  .
.
Решение.


Что и требовалось доказать.
Решим ещё одну задачу.
Задача.
В треугольнике 
 ,
,
 см,
см,
 см,
см,
 медиана.
медиана.
 .
Найти
.
Найти  ,
если
,
если  см.
см.
Решение.


Ответ. 13 см.
При решении задачи мы воспользовались свойством прямоугольного треугольника. Вспомним его подробнее.
В треугольнике ABC угол C равен 90° тогда и только тогда, когда медиана CM равна половине гипотенузы AB.
Отсюда можно сформулировать два утверждения.
Если в треугольнике ABC угол C равен 90°, то медиана CM равна половине гипотенузы АB.
И второе утверждение: если медиана CM треугольника ABC равна половине гипотенузы АB, то угол C данного треугольника равен 90°.
Действительно, если угол C= 90°, то треугольник не трудно достроить до прямоугольника. И зная, что диагонали прямоугольника равны и точкой пересечения делятся пополам, можно заметить, что CM действительно равно половине AB.

Ну, а если же в треугольнике ABC медиана CM равна половине стороны AB, то она делит данный треугольник на два равнобедренных треугольника.
Равные углы треугольника ACM обозначим за α. А равные углы треугольника BCM за β.
Запишем теорему о сумме углов треугольника для треугольника ABC. Получаем, что удвоенная сумма углов α и β равна 180°. Отсюда α+β= 90°.
А величина угла C как раз таки и равна α+β и, значит, равна 90°.
Подведём итоги нашего урока.
Сегодня мы познакомились с признаком перпендикулярности прямой и плоскости.
Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
Так же нами были рассмотрены примеры решения геометрических задач с помощью признака изученного на этом уроке.
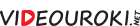
 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 7772
7772

