Сегодня мы будем говорить о том, где и как можно применять знания о подобии треугольников.
Для начала повторим всё, что мы знаем о подобии.
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
Выделяют три признака подобия треугольников: подобие по двум углам, подобие по двум сторонам и углу между ними, подобие по трём сторонам.
На уроках вы много раз сталкивались с задачами, где необходимо применить подобие треугольников. Сейчас мы с вами рассмотрим примеры решения задач на построение треугольников с применения подобия, то есть методом подобия.
Решение задач на построение треугольников методом подобия:
1. Построение треугольника подобного искомому
2. Построение искомого треугольника
Решим задачу на построение треугольника.
Задача. Построить треугольник, у которого два угла соответственно равны
двум данным углам, а биссектриса третьего угла равна данному отрезку
Построение.
1. 
2. 
3. биссектриса 
4. 
5. 

Доказательство.
1. 
2. 
Получаем, что треугольник ABC удовлетворяет всем условиям задачи.
Стоит обратить внимание на то, что сумма двух данных углов должна быть меньше 180º.
Аналогичным образом выполняются задачи на построение треугольника по двум углам и медиане, а также по двум углам и высоте.
Задача 1. Построить треугольник, у которого два угла соответственно равны
двум данным углам, а медиана проведённая, из третьего угла, равна данному отрезку.
Задача 2. Построить треугольник, у которого два угла соответственно равны
двум данным углам, а высота, проведённая из третьего угла, равна данному отрезку.

Сначала выбираем произвольный отрезок. На его концах строим углы равные данным. Получаем треугольник подобный искомому.
Проводим медиану или высоту из третьего угла.
От вершины C откладываем на них отрезки равные данному.
Проводим прямые, параллельные отрезку A1B1. Отмечаем точки пересечения полученной прямой со сторонами треугольника.

Искомые треугольники построены.
Сейчас мы рассмотрели примеры решения задач на построение треугольников методом подобия.
Также свойства подобных треугольников применяют при измерительных работах на местности. А именно: при определении высоты предмета и при определении расстояния до недоступной точки.
Рассмотрим примеры решения задач на определение высоты предмета.
Представим, что необходимо измерить высоту дерева, обозначим её B1C1. Понятно, что ни линейкой, ни верёвкой это сделать не возможно, так как до верхушки дерева никак нельзя дотянуться.
Поступим следующим образом. Возьмём шест высотой BC с вращающейся планкой на одном из концов, и направим планку на верхушку дерева.
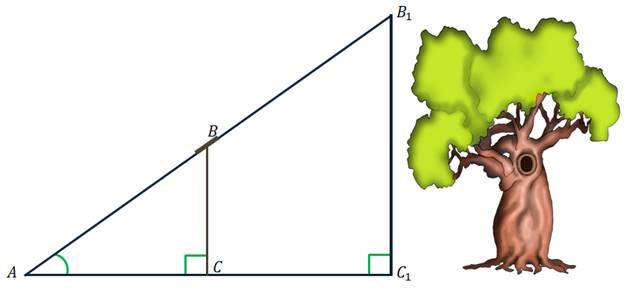
Отметим точкой А точку пересечения прямой BB1 с поверхностью земли.
Полученные треугольники ABC и AB1C1 подобны по двум углам, ведь угол А у них общий, а углы ACB и AC1B1 прямые:

Из подобия треугольников следует равенство отношений:

Допустим,  . Тогда искомая высота дерева:
. Тогда искомая высота дерева:
 .
.
Решим ещё одну задачу на определение высоты предмета.
Задача. Дерево отбрасывает тень длиной  м. А человек ростом
м. А человек ростом  см отбрасывает тень длиной
см отбрасывает тень длиной  см. Найдите высоту дерева.
см. Найдите высоту дерева.
Решение.
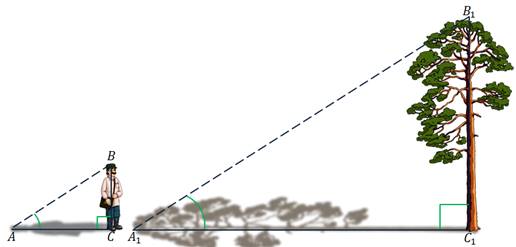
Рассмотрим прямоугольные треугольники, образованные объектами и их тенями.
Так как объекты находятся на одной географической широте, то угол падения солнечных лучей в обоих случая будет одинаковым. Углы C и C1 прямые.
Отсюда можем сделать вывод, что треугольники ABC и A1B1C1 подобны по двум углам. Значит, их соответствующие стороны пропорциональны и имеет место такое равенство:

Перед тем как подставлять известные величины переведём их в метры.



Перейдём к следующей группе задач. Определение расстояния до недоступной точки.
Предположим, нам нужно найти расстояние от некоторого пункта А до недоступной точки B.

Для этого на местности выбираем точку C, провешиваем отрезок AC и измеряем его длину. Далее измеряем углы А и C в треугольнике ABC. В этом нам поможет астролябия.
Астролябия — это угломерный прибор, служивший до 18 века для определения широт и долгот в астрономии, а также горизонтальных углов при землемерных работах.
Например, для определения угла, под которым наблюдатель видит звезду, направляющую этого прибора нужно расположить так, чтобы она одним своим концом указывала на глаз наблюдателя, а другим — на звезду. При этом горизонтальная ось должна быть параллельна линии горизонта.

Итак, измерив углы А и C, изобразим треугольник A1B1C1 так, чтобы угол А1 был равен углу А и угол C1 был равен углу C.

Измеряем длины сторон A1B1 и А1C1.



Если, зная длину отрезка AC, изобразить A1C1, например, с масштабом 1:1000, то можно значительно упростить вычисления.
Допустим AC=130 метрам, тогда A1C1 изобразим длиной в 130 миллиметров. Измерив A1B1 в миллиметрах, мы сразу получим длину АБ, но уже в метрах.
Задача. Для определения расстояния от точки А до недоступной точки B на местности выбрали точку C и измерили отрезок AC, углы BAC и ACB. Затем построили на бумаге треугольник A1B1C1 подобный треугольнику ABC. Найдите AB, если AC равно семи метрам, A1C1 — 2,8 сантиметра, A1B1 — 3,4 сантиметра.
Из подобия треугольников следует равенство отношений. Отсюда выразим AB.
Подставим известные значения, переведя их предварительно в метры.

 ,
,  ,
,  .
.
Ответ: 
Подведём итоги урока.
Сегодня мы с вами знакомились с практическими приложениями подобия треугольников.
А именно рассмотрели примеры решения задач на построение треугольников методом подобия. Он состоит из двух этапов: построение треугольника подобного искомому и построение искомого треугольника.
А также познакомились с такими измерительными работами на местности как «определение высоты предмета» и «определение расстояния до недоступной точки».
 Получите свидетельство
Получите свидетельство Вход
Вход




 0
0 17179
17179

