Вопросы занятия:
· вспомнить основные формулы, связывающие элементы треугольника;
· доказать, что сумма углов треугольника равна 180°;
· вспомнить, какой угол называют внешним углом треугольника;
· доказать теорему о внешнем угле треугольника;
· поговорить о соотношениях между углами и сторонами треугольника;
· повторить неравенство треугольника.
Материал урока
Начнём мы разговор с истории.
Блез Паскаль, великий французский учёный XVII века, заметил, что у всех треугольников сумма трёх углов равна 180о. И у него возник вопрос: «Как это доказать?»

Тогда он отрезал ножницами два уголка треугольника и приложил их к третьему углу. В результате получился развёрнутый угол, градусная мера которого, как вам уже известно, равна 180о. Это было его первое собственное открытие.

Итак, давайте сформулируем и докажем теорему о сумме углов треугольника.
Звучит она так. Сумма углов треугольника равна ста восьмидесяти градусам.
Доказательство. Пусть  –
произвольный треугольник. Докажем, что сумма углов
–
произвольный треугольник. Докажем, что сумма углов  .
.

Проведём прямую а через точку
В параллельно стороне  .
Углы
.
Углы  ,
,
 –
внутренние накрест лежащие углы при параллельных прямых а и
–
внутренние накрест лежащие углы при параллельных прямых а и  и
секущей
и
секущей  .
А значит,
.
А значит,  .
Углы
.
Углы  ,
,
 являются
внутренними накрест лежащими при параллельных прямых а и
являются
внутренними накрест лежащими при параллельных прямых а и  и
секущей
и
секущей  .
Следовательно,
.
Следовательно,  .
.
Сумма градусных мер углов  ,
,
 и
и
 равна
градусной мере развёрнутого угла с вершиной в точке В, то есть
равна
градусной мере развёрнутого угла с вершиной в точке В, то есть  .
А так как
.
А так как  ,
,
 ,
то получаем, что
,
то получаем, что  .
То есть
.
То есть  .
.
Теорема доказана.
Из теоремы следует, что все углы равностороннего треугольника равны по 60о.

Сумма острых углов прямоугольного треугольника равна 90о.

А теперь давайте вспомним, какой угол называют внешним углом треугольника.
Определение.
Внешним углом треугольника называют угол, смежный с каким-либо углом треугольника.

Например,  –
внешний угол треугольника
–
внешний угол треугольника  ,
смежный с углом
,
смежный с углом  .
.
 –
внешний угол, смежный с углом
–
внешний угол, смежный с углом  .
.
Сформулируем теорему о внешнем угле треугольника.
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
Доказательство. Пусть  –
произвольный треугольник. Докажем, что градусная мера
–
произвольный треугольник. Докажем, что градусная мера  ,
не смежных с ним.
,
не смежных с ним.
Сумма градусных углов  равна
градусной мере развёрнутого угла, то есть
равна
градусной мере развёрнутого угла, то есть  .
А по теореме о сумме градусных мер углов треугольника
.
А по теореме о сумме градусных мер углов треугольника  .
Из полученных двух равенств следует, что
.
Из полученных двух равенств следует, что  .
.
Что и требовалось доказать.
Задача.
На рисунке:  ,
а
,
а  .
Найдите градусную меру
.
Найдите градусную меру  .
.
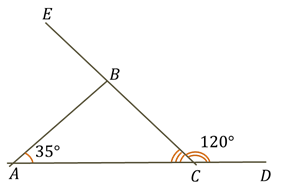
Так как углы  ,
,
 –
смежные, то
–
смежные, то  .
Нам известно, что
.
Нам известно, что  ,
тогда
,
тогда  .
.
Искомый угол  является
внешним углом нашего треугольника, смежным с углом
является
внешним углом нашего треугольника, смежным с углом  .
А значит, его градусная мера равна
.
А значит, его градусная мера равна  .
Следовательно, угол
.
Следовательно, угол  .
.
Напомним, что по величине углов выделяют остроугольные, прямоугольные и тупоугольные треугольники. А также отметим, что сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны – катетами.

А теперь мы сформулируем и докажем теорему о соотношениях между сторонами и углами треугольника.
В треугольнике против большей стороны лежит больший угол, а против большего угла лежит большая сторона.
Доказательство. Сначала
докажем, что против большей стороны лежит больший угол. Возьмём некоторый
треугольник  .
Пусть у него сторона
.
Пусть у него сторона  .
Отложим сторону
.
Отложим сторону  на
стороне
на
стороне  ,
то есть отрезок
,
то есть отрезок  .
.

Так как получается, что треугольник  –
равнобедренный, то
–
равнобедренный, то  (как
углы при основании равнобедренного треугольника).
(как
углы при основании равнобедренного треугольника).
В треугольнике  угол
угол
 ,
так как внешний угол больше любого внутреннего, не смежного с ним. В
треугольнике
,
так как внешний угол больше любого внутреннего, не смежного с ним. В
треугольнике  угол
угол  .
Из последнего неравенства и из того, что
.
Из последнего неравенства и из того, что  ,
а
,
а  ,
следует, что
,
следует, что  .
.
То есть, против большей стороны  лежит
больший
лежит
больший  .
.
Что и требовалось доказать.
Теперь докажем, что против большего угла лежит большая сторона.
Пусть  треугольника
треугольника
 .
Если предположить, что сторона
.
Если предположить, что сторона  ,
то по доказанной первой части данной теоремы
,
то по доказанной первой части данной теоремы  .
Получили противоречие.
.
Получили противоречие.
Если сторона  ,
то получается, что треугольник
,
то получается, что треугольник  равнобедренный,
а тогда
равнобедренный,
а тогда  .
Снова противоречие.
.
Снова противоречие.
Так как в каждом из предыдущих
случаев наше предположение неверно, тогда получаем, что  .
.
Теорема доказана.
Из только что доказанной теоремы вытекают следствия.
В прямоугольном треугольнике  гипотенуза
гипотенуза
 больше
катетов
больше
катетов  и
и
 .
.

Действительно, верно, так как гипотенуза лежит против прямого угла, а катеты – против острых, градусная мера которых меньше 90о.
Другое следствие называют признаком равнобедренного треугольника.
Если два угла треугольника равны, то треугольник равнобедренный.
Доказательство. Пусть  треугольник,
у которого
треугольник,
у которого  .
Докажем, что равны стороны
.
Докажем, что равны стороны  ,
лежащие против этих углов.
,
лежащие против этих углов.
Предположим, что сторона  .
Тогда по предыдущей теореме
.
Тогда по предыдущей теореме  ,
лежащий против большей стороны
,
лежащий против большей стороны  ,
будет
,
будет  ,
лежащего против меньшей стороны
,
лежащего против меньшей стороны  .
Получили противоречие условию равенства углов
.
Получили противоречие условию равенства углов  .
.
Следовательно, наше предположение
неверно и стороны  равны,
то есть треугольник
равны,
то есть треугольник  является
равнобедренным.
является
равнобедренным.
Что и требовалось доказать.
Задача.
В треугольнике  :
:
 ,
а
,
а  .
Верно ли, что сторона
.
Верно ли, что сторона  больше
каждой из сторон
больше
каждой из сторон  и
и
 ?
?

По теореме о сумме углов
треугольника сумма углов  .
Выразим из этого равенства угол
.
Выразим из этого равенства угол  .
.

Затем подставим известные значения
углов  ,
а
,
а  и
найдём градусную меру угла
и
найдём градусную меру угла  .
Она равна:
.
Она равна:

А теперь, воспользовавшись теоремой о соотношениях между сторонами и углами треугольника, выясним, какая же из сторон нашего треугольника имеет большую длину.
Так как против большего угла лежит
большая сторона, а в нашем случае большую градусную меру имеет угол  ,
то большей стороной треугольника является сторона
,
то большей стороной треугольника является сторона  .
Поэтому, ответ на вопрос задачи будет таким: «нет, неверно, что сторона
.
Поэтому, ответ на вопрос задачи будет таким: «нет, неверно, что сторона  больше
каждой из сторон
больше
каждой из сторон  и
и
 ».
».
А теперь давайте сформулируем и докажем теорему, которая имеет название неравенство треугольника.
Длина любой стороны треугольника меньше суммы двух других его сторон.
Доказательство. Пусть  –
произвольный треугольник. Докажем, что длина стороны
–
произвольный треугольник. Докажем, что длина стороны  .
.

Опустим высоту  на
большую сторону
на
большую сторону  .
Получили два прямоугольных треугольника:
.
Получили два прямоугольных треугольника:  и
и  .
Напомним, что в любом прямоугольном треугольнике катет меньше гипотенузы. Тогда
можем записать, что в треугольнике
.
Напомним, что в любом прямоугольном треугольнике катет меньше гипотенузы. Тогда
можем записать, что в треугольнике  катет
катет
 ,
а в треугольнике
,
а в треугольнике  катет
катет
 .
.
Сложим эти два неравенства.

Обратите внимание, в левой части
неравенства записана сумма сторон  .
О она в свою очередь равна стороне
.
О она в свою очередь равна стороне  .
.
Т.е. получили, что  .
.
Теорема доказана.
Из доказанной теоремы следует, что для любых трёх точек А, В и С, не лежащих на одной прямой, справедливы следующие неравенства:


И ещё одно следствие из теоремы.
Длина каждой стороны треугольника больше разности длин двух других его сторон.


Задача.
Докажите, что сторона  меньше
его полупериметра.
меньше
его полупериметра.
Доказательство. Каждая
сторона треугольника меньше суммы двух других его сторон. В нашем треугольнике  для
стороны
для
стороны  имеем
следующее неравенство:
имеем
следующее неравенство:  .
.
Прибавим к обеим частям этого
неравенства  и
получим:
и
получим:

Заметим, правая часть полученного
неравенства и есть полупериметр треугольника  .
.

Что и требовалось доказать.
Итоги урока
На этом уроке мы вспоминали «основные формулы, связывающие элементы треугольника». Доказали, что сумма углов треугольника равна ста восьмидесяти градусам. Вспомнили, какой угол называют внешним углом треугольника, а затем доказали теорему о внешнем угле треугольника. Поговорили о соотношениях между углами и сторонами треугольника. И завершили повторение неравенством треугольника.
 Получите свидетельство
Получите свидетельство Вход
Вход




 0
0 1949
1949

