Показательная функция, ее свойства и график

Вопросы занятия:

·     ввести показательную функцию как обратную к степенной;

·     рассмотреть свойства и графики показательной функции, в зависимости от основания.

Материал урока

До сегодняшнего урока мы с вами рассматривали степенные функции, основанием которых была переменная x, а показателем произвольное число а. Эти функции мы рассмотрели с различными показателями и изучили их свойства, посмотрели, как себя ведут графики этих функций.

А сегодня давайте попробуем поменять местами основание и показатель степени и рассмотрим выражение: a^x. Поскольку каждому x ставится в соответствие единственное выражение a^x, то можно сказать, что задана функция:

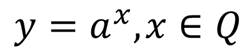
Такую функцию называют показательной. Давайте теперь попробуем определить, для любого ли а можно задать такую функцию?

Напомним, что степенную функцию мы определяли только на промежутке [0; + ∞), причём, в случае отрицательного а, 0 исключался из этого промежутка. Это мы обосновывали тем, что отрицательное число можно возвести лишь в некоторые рациональные степени, а 0 нельзя возводить в неположительную степень. Такие же ограничения накладываются на основание показательной функции, то есть в качестве а можно брать только положительные числа. Причём ещё исключается число 1. Потому что единица в любой степени равна единице.

Теперь давайте определим множество, которое будет являться областью определения данной функции.

Мы сказали, что функция определена на множестве рациональных чисел, но ещё есть иррациональные числа, как же быть с ними?

Давайте рассмотрим частный случай показательной функции:

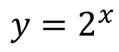
И попробуем вычислить значение выражения:

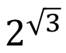
Мы знаем, что:

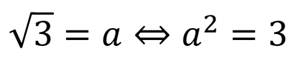
С помощью калькулятора несложно вычислить приближенное значение этого выражения:

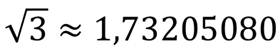
Как же вычислить значение степени с иррациональным показателем? Рассмотрим последовательность рациональных чисел:

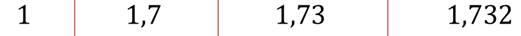
И будем находить значение выражения 2^x для каждого из этих чисел:

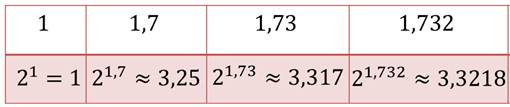
Мы получили возрастающую последовательность приближений, соответственно возрастает и вторая последовательность. Все члены этой последовательности – это положительные числа, меньшие два в квадрате, то есть последовательность ограничена. По теореме Вейерштрасса, если последовательность возрастает и ограничена, то она имеет предел. Этот предел и будет значением числового выражения:

Подводя итог нашим рассуждений, можно записать определение.

Определение.

Пусть a > 1 и α = a, a₁a₂a₃…a_n… – положительное иррациональное число (бесконечная непериодическая дробь). Составим последовательность десятичных приближений числа a по недостатку:

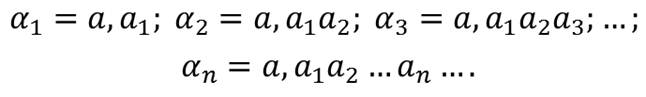
Тогда предел последовательности

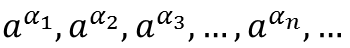
обозначают

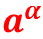
и называют степенью с иррациональным показателем.

Если a > 1 и α < 0 – иррациональное число, то под выражением:

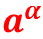
будем понимать выражение:

Если 0 < α < 1, то под выражением:

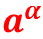
будем понимать выражение:

.

Таким образом, показательная функция определена на множестве действительных чисел.

D(y = a^x) = ( – ∞; + ∞)

Вернёмся к рассмотренной выше функции:

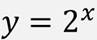
Построим график этой функции.

Для этого построим таблицу значений этой функции, отметим полученные точки на координатной плоскости, соединим полученные точки и получим график функции:

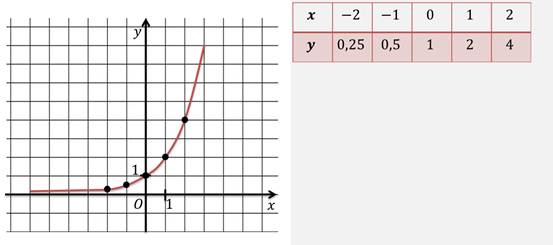
Такой же вид будет иметь и график функции вида:

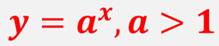
С помощью графика легко записать основные свойства функции.

Областью определения будет вся числовая прямая.

Областью значений будет промежуток (0; + ∞).

Функция не является ни чётной, ни нечётной.

Функция возрастает на всей области определения.

Функция не ограничена сверху, но ограничена снизу.

Функция не имеет ни наибольшего, ни наименьшего значений.

Функция непрерывна на всей области определения.

Функция выпукла вниз.

Рассмотрим теперь функцию:

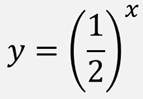
Построим график этой функции.

Для этого построим таблицу значений этой функции, отметим полученные точки на координатной плоскости, соединим полученные точки и получим график функции.

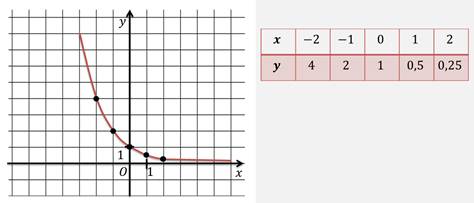
Такой же вид будет иметь и график функции:

С помощью графика легко записать основные свойства функции.

Областью определения будет вся числовая прямая.

Областью значений будет промежуток от нуля до плюс бесконечности.

Функция не является ни чётной, ни нечётной.

Функция убывает на всей области определения.

Функция не ограничена сверху, но ограничена снизу.

Функция не имеет ни наибольшего, ни наименьшего значений.

Функция непрерывна на всей области определения.

Функция выпукла вниз.

Если мы построим графики функций на одном графике,

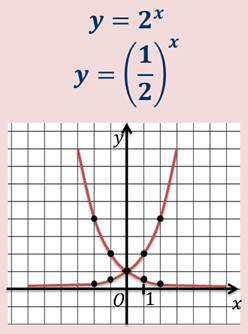
то заметим, что графики этих функций симметричны относительно Oy.

Аналогично будут симметричны и графики функций:

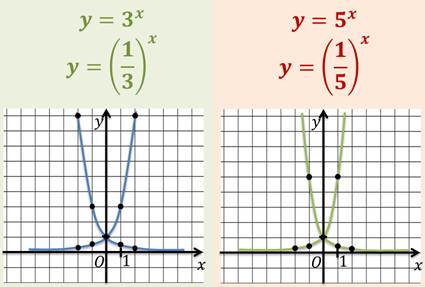
Теперь давайте дадим чёткое определение показательной функции и выделим наиболее важные её свойства.

Функцию вида:

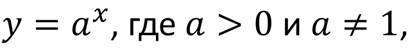
называют показательной функцией.

Запишем основные свойства показательной функции.

График функции и саму функцию называют экспонентой.

По графику легко увидеть, что ось Ox будет являться горизонтальной асимптотой экспоненты.

С показательными функциями связаны многие экономические, биологические, физические законы.

Сделаем важное замечание: не будем путать понятия степенная и показательная функция. Напомним, что функция вида y = x^a называется степенной, а функция y = a^x – это показательная функция.

А функцию y =x^x не считают ни показательной, ни степенной (её иногда называют показательно-степенной).

Рассмотрим пример.

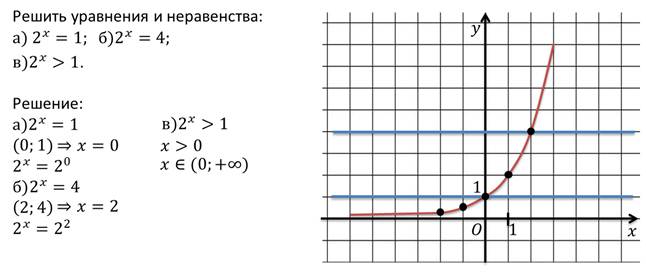
Сформулируем теоремы.

Теорема 1.

Если a > 1, то равенство a^t = a^s справедливо тогда и только тогда, когда t = s.

Теорема 2.

Если a > 1, то неравенство a^x > 1 справедливо тогда и только тогда, когда x > 0; неравенство a^x < 1, справедливо тогда и только тогда, когда x < 0.

Доказывать эти теоремы мы не будем.

Рассмотрим ещё один пример.

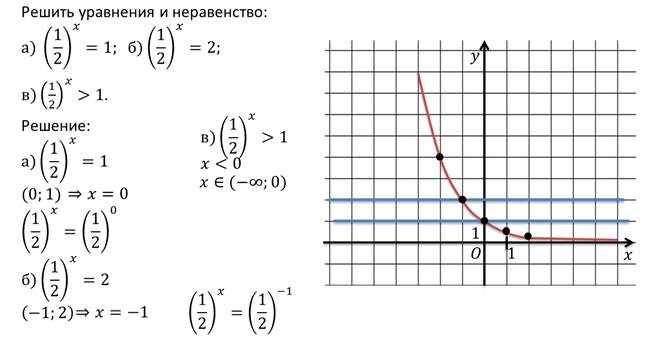
Сформулируем ещё две теоремы.

Теорема 1.

Если 0 < a < 1, то равенство a^t = a^s справедливо тогда и только тогда, когда t = s.

Теорема 2.

Если 0 < a < 1, то неравенство a^x > 1 справедливо тогда и только тогда, когда

x < 0; неравенство a^x < 1, справедливо тогда и только тогда, когда x > 0.

Давайте повторим главное.

Функцию вида:

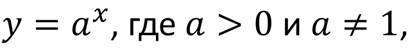
называют показательной функцией.

Запишем основные свойства показательной функции.

График функции и саму функцию называют экспонентой.