Применение определенного интеграла

ГАПОУ «Оренбургский областной медицинский колледж»

Методическая разработка

для преподавателя

по дисциплине БД.04 МАТЕМАТИКА

«Применение определенного интеграла»

Оренбург – 2021

Рассмотрено и одобрено

на заседании ПЦК

общеобразовательных дисциплин

Протокол № ___ от «__»_______

Председатель ПЦК

_________________ Н.В. Лапина

Автор:

Е.В. Данилова, преподаватель математики высшей квалификационной категории.

Аннотация:

Методическая разработка предназначена для преподавателей математики. Содержит план занятия, конспект занятия, список источников информации. В разработке представлены различные случаи нахождения площадей плоских фигур с примерами. Предложены различные формы работы и методы контроля знаний и умений по теме.

Содержание

Технологическая карта занятия

Тема: «Применение определенного интеграла»

Цели:

Обучающийся научится:

• Оперировать на базовом уровне понятиями: первообразная функции, неопределенный и определенный интеграл, формула Ньютона-Лейбница, криволинейная трапеция;

• Определять общий вид первообразной функции;

• Вычислять определенный интеграл;

• Вычислять площадь криволинейной трапеции.

Обучающийся получит возможность научиться:

• Оперировать понятиями: первообразная функции, неопределенный и определенный интеграл, формула Ньютона-Лейбница, криволинейная трапеция;

• находить общий вид первообразной, неопределенный интеграл;

• находить первообразную функции проходящую через точку;

• вычислять определенный интеграл с применением формулы Ньютона-Лейбница;

• вычислять площадь криволинейной трапеции и фигуры, ограниченной линиями.

Развивающая

• способствовать формированию умения анализировать, определять вид фигуры и выбирать формулу, действовать по алгоритму.

Воспитательная

• Воспитывать дисциплинированность, аккуратность, сознательное отношение к учебе.

Методическая

• Ввести понятие криволинейной трапеции и фигуры, ограниченной линиями.

• Рассмотреть разнообразные случаи расположения фигуры в системе координат и формулы для вычисления площади.

Тип занятия: изучение нового и закрепление.

Вид занятия: практическое.

Формы организации учебной деятельности: групповая, индивидуальная.

Методы обучения: словесные, наглядные, практические, решение задач, алгоритмизированные.

Формы контроля: фронтальный опрос, индивидуальный опрос у доски, решение задач.

Межпредметные связи: физика.

Внутрипредметные связи: производная, функции, формула Ньютона-Лейбница.

Оборудование: доска классная, мел, линейка, телевизор с USB.

Оснащение:

Методическое оснащения занятия:

Рабочая программа учебной дисциплины БД.04 Математика, тематический план, технологическая карта занятия, методическое пособие для преподавателя.

Дидактическое оснащение занятия: учебник.

Литература и интернет-источники:

Алимов Ш. А., Колягин Ю.М., Ткачёва М.В. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровень). Просвещение, 2018г.

План:

1. Организационный момент (2-3 мин).

2. Постановка целей и задач, мотивация (5-7 мин).

3. Актуализация знаний (8-10 мин).

Фронтальный опрос.

Индивидуальный письменный опрос у доски.

1. Изучение нового (40-45 мин).

• Криволинейная трапеция.

• Площадь криволинейной трапеции.

• Различные случаи расположения фигуры в системе координат и их площади.

1. Первичное закрепление (20-25 мин).

2. Домашнее задание (1-2 мин).

3. Рефлексия (2-3 мин).

Ход занятия

1. Организационный момент (2-3 мин).

Проверка присутствующих и их готовности к занятию.

1. Постановка целей и задач, мотивация (5-7 мин).

Обоснование важности изучения и умения применять определенные интегралы для решения практических задач. Приведение примеров применения определенного интеграла в жизни. Просмотр видео (Приложение 1).

1. Актуализация знаний (8-10 мин).

3.1.Фронтальный опрос.

Вопросы:

• Перечислите основные формулы первообразных функций.

• Дайте определение первообразной функции.

• Дайте определение интеграла.

• Перечислите свойства интегралов.

• Дайте определение определенного интеграла.

3.2.Индивидуальный письменный опрос у доски.

У доски работают 2 человека, выполняя одни и те же задания на разных разворотах доски.

Задание. Запишите формулу Ньютона-Лейбница и вычислите определенные интегралы.

1) ; 2) ; 3) .

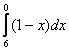1. Изучение нового (40-45 мин).

4.1. Криволинейная трапеция.

О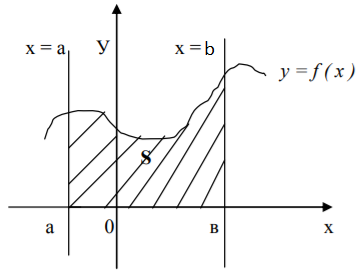 пределение: Криволинейной трапецией называется фигура, ограниченная графиком непрерывной функции, прямыми х = а и х = b и осями координат.

Плоская фигура – это фигура, лежащая в плоскости ХОУ и состоящая из криволинейных трапеций.

4.2. Площадь криволинейной трапеции.

Для вычисления площади криволинейной трапеции нам понадобятся:

1. Определённый интеграл от функции, задающей кривую, которая ограничивает криволинейную трапецию сверху. И здесь возникает первый существенный нюанс: криволинейная трапеция может быть ограничена кривой не только сверху, но и снизу. Как действовать в этом случае? Просто, но это важно запомнить: интеграл в этом случае берётся со знаком минус.

2. Пределы интегрирования a и b, которые находим из уравнений прямых, ограничивающих фигуру слева и справа: x = a, x = b, где a и b - числа.

3. Кривая, которая ограничивает криволинейную трапецию сверху (или снизу) должна быть графиком непрерывной и неотрицательной функции y = f(x).

4. Значения "икса" должны принадлежать отрезку [a; b].

5. Боковые отрезки могут вырождаться в точки. Если вы увидели такую фигуру на чертеже, это не должно вас смущать, так как эта точка всегда имеет своё значение на оси абсцисс. А значит с пределами интегрирования всё в порядке.

Алгоритм вычисления площади плоской фигуры:

1. Построить графики заданных функций.

2. Найти точки пересечения графиков функций. Абсциссы точек пересечения графиков функций будут являться пределами интегрирования.

3. Представить площадь плоской фигуры как сумму или разность площадей криволинейных трапеций.

4. Вычислить площадь каждой трапеции по формуле Ньютона – Лейбница.

4.3. Различные случаи расположения фигуры в системе координат и их площади.

Итак, площадь s криволинейной трапеции может быть вычислена по формуле

(1).

Если же f(x) ≤ 0 (график функции расположен ниже оси абсцисс), то площадь криволинейной трапеции может быть вычислена по формуле

(2)

Есть ещё случаи, когда и верхняя, и нижняя границы фигуры - функции, соответственно y = f(x) и y = φ(x), то площадь такой фигуры вычисляется по формуле

(3)

Случаи, когда площадь фигуры может быть вычислена по формуле (1).

П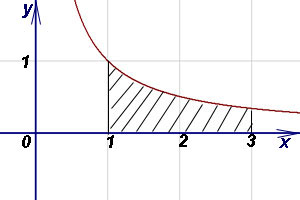 ример 1. Найти площадь фигуры, ограниченной графиком функции 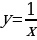, осью абсцисс и прямыми x = 1, x = 3.

Решение. Так как y = 1/x 0 на отрезке [1; 3], то площадь криволинейной трапеции находим по формуле (1):

.

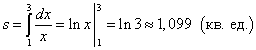П ример 2. Найти площадь фигуры, ограниченной графиком функции 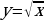, осью абсцисс и прямой x = 4.

Решение. Фигура, соответствующая условию задачи - криволинейная трапеция, у которой левый отрезок выродился в точку. Пределами интегрирования служат 0 и 4. Поскольку 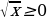, по формуле (1) находим площадь криволинейной трапеции:

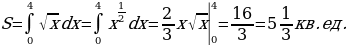
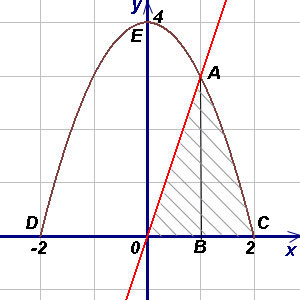
Пример 3. Найти площадь фигуры, ограниченной линиями 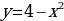, , 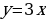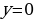и находящейся в 1-й четверти.

Решение. Чтобы воспользоваться формулой (1), представим площадь фигуры, заданной условиями примера, в виде суммы площадей OAB и криволинейной трапеции ABC. При вычислении площади OAB пределами интегрирования служат абсциссы точек O и A, а для фигуры ABC - абсциссы точек A и C (A является точкой пересечения прямой OA и параболы, а C - точкой пересечения параболы с осью абсцисс). Решая совместно (как систему) уравнения прямой и параболы, получим 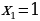(абсциссу точки A) и 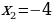(абсциссу другой точки пересечения прямой и параболы, которая для решения не нужна). Аналогично получим 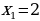, 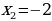(абсциссы точек C и D). Теперь у нас есть всё для нахождения площади фигуры. Находим:

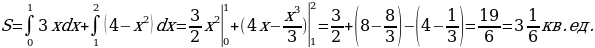
П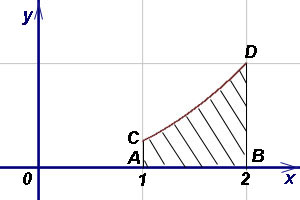 ример 4. Найти площадь криволинейной трапеции ACDB, если уравнение кривой CD 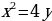и абсциссы A и B соответственно 1 и 2.

Решение. Выразим данное уравнение кривой через переменную y: 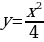Площадь криволинейной трапеции находим по формуле (1):

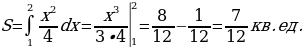
Случаи, когда площадь фигуры может быть вычислена по формуле (2).

П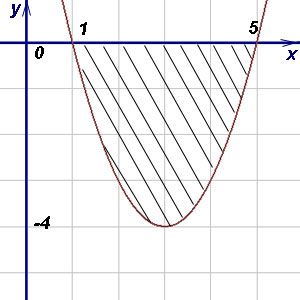 ример 5. Найти площадь фигуры, ограниченной параболой 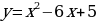и осью абсцисс.

Решение. Данная фигура расположена ниже оси абсцисс. Поэтому для вычисления её площади воспользуемся формулой (2). Пределами интегрирования являются абсциссы 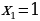и 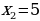точек пересечения параболы с осью абсцисс. Следовательно,

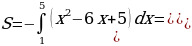
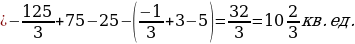
П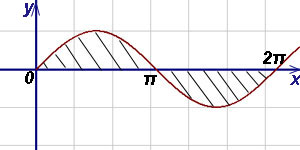 ример 6. Найти площадь, заключённую между осью абсцисс и двумя соседними волнами синусоиды.

Решение. Площадь данной фигуры можем найти по формуле (2):

.

Найдём отдельно каждое слагаемое:

.

.

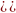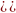Окончательно находим площадь: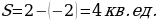

Случаи, когда площадь фигуры может быть вычислена по формуле (3).

П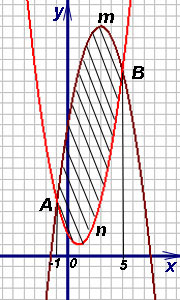 ример 7. Найти площадь фигуры, заключённой между параболами 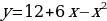и .

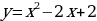Решение. Требуется вычислить площадь фигуры, у которой боковые отрезки выродились в точки A и B пересечения парабол. Решая совместно (как систему) уравнения парабол, находим их абсциссы: 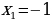и .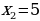

На отрезке [-1; 5] получаем 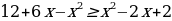. Следовательно, по формуле (3) находим площадь фигуры:

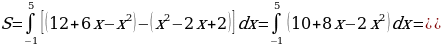
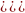
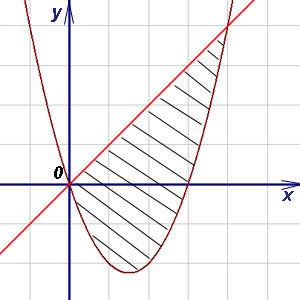
П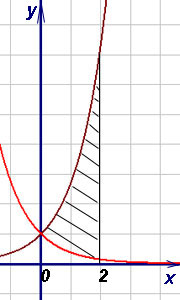 ример 8. Найти площадь фигуры, ограниченной графиками функций 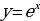, 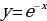и прямыми 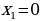и .

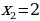Решение. Так как 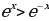на отрезке [0; 2], то, используя для нахождения площади формулу (3), получим

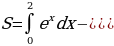
Пример 9. Найти площадь фигуры, заключённой между параболой 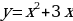и прямой .

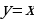Решение. Находим абсциссы точек пересечения параболы и прямо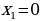й: и 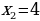. Так как 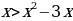на отрезке [0; 4], то по формуле (3) находим площадь фигуры:

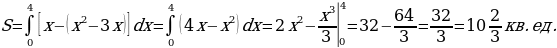
1. Первичное закрепление (20-25 мин).

1. Вычислить площадь фигуры, ограниченной линиями х + у – 4 =0, у = 0, х = - 3, х = 2.

2. Вычислить площадь фигуры, ограниченной линиями х – 2 у + 4 = 0, х + у = 5, у = 0.

3. Найдите площадь фигуры, ограниченной линиями, изображенными на рисунке.

А)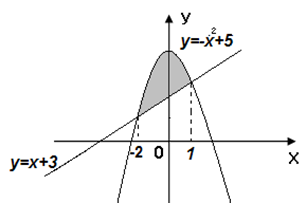 ; Б)

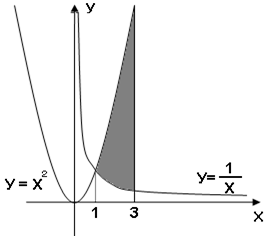
1. Домашнее задание (1-2 мин).

§56,58.

Вычислить площадь фигуры, ограниченной параболой 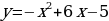  и прямыми  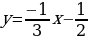, x=1, x=4.

СВР: Подготовка сообщения по теме «Применение определенного интеграла в физике».

1. Рефлексия (2-3 мин). Ответ на вопросы студентов.

Список источников

Основные:

1. Алимов Ш. А., Колягин Ю.М., Ткачёва М.В. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровень). Просвещение, 2018г.

2. https://www.youtube.com/watch?v=y1B3mypflRE

Дополнительные:

1. Колмогоров А.Н. Алгебра и начала математического анализа: Учебник для 10-11 кл. общеобразовательных учреждений / А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницин и др. – М.: Просвещение, 2010.

2. Богомолов Н.В. Математика: учебник для ссузов / Н.В. Богомолов, П.И. Самойленко. – 7-е изд., стереотип. – М.: Дрофа, 2010.

6