Друзья, наше сегодняшнее занятие будет посвящено квадратам, которые на протяжении уже очень долгого времени являются объектом пристального изучения многих математиков.
Давайте с вами рассмотрим квадрат, который разбит на 9 маленьких квадратиков. В каждый квадратик вписано число от 1 до 9.

Сложив числа в каждом горизонтальном ряду этого квадрата, получим 15 Сложив числа в каждом его вертикальном ряду, тоже получим 15. Сложив числа по диагонали, которая идёт из верхнего левого угла в нижний правый угол этого квадрата, снова получим 15. Сложив числа по диагонали, которая идёт из верхнего правого угла квадрата в нижний левый угол, опять получим 15.
Такой квадрат является примером квадрата, который в математике называют магическим (или волшебным). А так как он размером 3 на 3 клетки, то его называют магическим квадратом третьего порядка.
Таким образом, квадрат, разбитый на определённое количество маленьких квадратиков (или клеток), в которые вписаны числа так, что суммы чисел в каждой строке, в каждом столбце, а также на каждой из двух диагоналей всегда одинаковы, называется магическим.
При этом сумма чисел в каждой строке, в каждом столбце и на каждой диагонали называется магической константой. Она обозначается большой буквой М.
Магическая константа этого квадрата равна 15.
Магические квадраты были известны китайцам и индийцам уже несколько тысячелетий назад. Встречаются китайские амулеты с магическими квадратами, в которых ещё нет цифр, но есть определённое количество проколов или углублений.
Посмотрите на магический квадрат, который считается самым древним. Он появился в Китае примерно за 2200 лет до нашей эры и до сих пор используется в качестве талисмана под названием Ло-Шу.

Из рассмотренного магического квадрата третьего порядка перестановкой строк и столбцов, а также путём поворота можно получить ещё 7 квадратов, каждый из которых будем магическим с магической константой, равной 15.

Сейчас посмотрите на такой квадрат третьего порядка.

Сложив числа в любой его строке, получим 15. Сложив числа в любом его столбце, тоже получим 15. А вот сложив числа по диагонали, которая идёт из верхнего левого угла в нижний правый угол квадрата, получим не 15, а 24. Сложив числа по диагонали, которая идёт из верхнего правого угла квадрата в его нижний левый угол, получим 18.
Таким образом, в данном квадрате равны суммы чисел только в строках и в столбцах, а значит, он является волшебным только наполовину. Ребята, такие квадраты называют полумагическими.
Теперь посмотрите на квадрат размером 4 на 4 клетки, который заполнен числами от 1 до 16.

Сложив числа в каждой строке этого квадрата, мы получим 34. Сложив числа в каждом его столбце, мы тоже получим 34. Сложив числа по диагонали, которая идёт из верхнего левого угла в нижний правый угол этого квадрата, снова получим 34. Сложив числа по диагонали, которая идёт из верхнего правого угла в нижний левый угол, опять получим 34. Следовательно, можно сделать вывод, что данный квадрат является магическим квадратом четвёртого порядка с магической константой, равной 34.
Этот волшебный квадрат четвёртого порядка изображён на гравюре немецкого художника Альбрехта Дюрера, которая была создана в 1514 году. Обратите внимание, что два средних числа в нижнем ряду квадрата указывают на год создания гравюры.
Существует 880 вариантов магических квадратов четвёртого порядка, заполненных числами от 1 до 16.
Посмотрите на магический квадрат пятого порядка, который заполнен числами от 1 до 25. Его магическая константа равна 65.

Вот магический квадрат шестого порядка. Он заполнен числами от 1 до 36. Его магическая константа равна 111.

Это магический квадрат седьмого порядка, который заполнен числами от 1 до 49. Его магическая константа равна 175.

А теперь перед вами квадрат восьмого порядка, заполненный числами от 1 до 64. Он был составлен в 18 веке Леонардом Эйлером – великим математиком и механиком. Волшебство этого квадрата заключается в том, что сумма чисел в каждой его строке равна 260 и сумма чисел в каждом его столбце тоже равна 260. А сумма чисел половины каждого ряда равна 130. При этом суммы чисел в ячейках, образующих диагонали, не равны 260 и даже не равны между собой.

Ребята, а вот магических квадратов второго порядка не существует.
Сейчас давайте из рассмотренного ранее магического квадрата третьего порядка получим квадрат, в центре которого будет не число 5, а число 14.

Для этого из 14 вычтем 5. Получим 9. Затем к каждому числу квадрата прибавим 9. Выполнив сложение в каждой клеточке, получим новый магический квадрат, в центре которого расположено число 14. Магическая константа этого квадрата равна 42.

Убедиться в этом можно, найдя суммы чисел в каждой строке полученного квадрата, в каждом его столбце, а также на диагоналях.
Теперь возьмём магический квадрат Альбрехта Дюрера и попробуем получить из него квадрат, у которого магическая константа будет равна 50.
Итак, у квадрата, изображённого на гравюре Альбрехта Дюрера, магическая константа равна 34. Вычтем 34 из 50. Получим 16. Это значит, что у нового квадрата магическая константа будет на 16 больше, чем у данного.
Мы знаем, что магическая константа – это сумма чисел в каждой строке, в каждом столбце и на каждой диагонали.
Так как в каждом ряду и в каждом столбце квадрата четыре клетки, то разделим 16 на 4. Получим 4.
Прибавим 4 каждому числу квадрата. Выполним сложение в каждой клеточке и получим новый магический квадрат, у которого магическая константа равна 50.

Убедимся в этом, найдя суммы чисел в каждой строке полученного квадрата, в каждом его столбце, а также на диагоналях.
Задание. В пустые клетки квадрата размером 3 на 3 вставьте числа 2, 6, 8, 12, 14, 16 так, чтобы квадрат стал магическим.

Решение. В первую очередь найдём сумму всех чисел, которые должны быть размещены в клетках квадрата. Это сумма чисел, которые уже записаны в клетках квадрата и которые даны в условии задачи. Выполним сложение и получим 90. Получается, что сумма всех чисел квадрата – 90. Она складывается из сумм в каждом ряду.
В квадрате три ряда и сумма чисел в каждом ряду одинакова. Следовательно, 90 надо разделить на 3. Получим 30. Это число и будет магической константой данного квадрата.
Давайте начнём заполнять квадрат. Итак, посмотрите на числа, стоящие в нижней строке квадрата. Неизвестно только одно число. Чтобы его найти, надо из 30 вычесть 4 и 18. Выполним вычитание и получим 8.
Теперь посмотрите на числа, которые стоят во втором столбце. Неизвестно только одно число. Найдём его. Так как сумма чисел в каждом столбце квадрата также равна 30, то из 30 вычтем 10 и 18. Получим 2.

Далее посмотрите на числа, стоящие вдоль одной из диагоналей. Неизвестно одно число. Сумма чисел на каждой диагонали равна 30. Значит, из 30 надо вычесть 10 и 8. Выполним вычитание и получим 12.
Посмотрите на числа, которые стоят вдоль другой диагонали. Также неизвестно только одно число. Чтобы его найти, из 30 вычтем 4 и 10. Получим 16.

Затем найдём число, которое должно быть вот в этой клетке.

Вычтем 12 и 4 из 30. Получим 14.
Чтобы заполнить последнюю пустую клеточку, из 30 вычтем 16 и 8. Выполним вычитание и получим 6.

Вот таким образом, мы вписали данные числа в квадрат так, что он
стал магическим с магической константой, равной 30. Убедиться в этом можно,
найдя суммы чисел в каждой строке полученного квадрата, в каждом его столбце, а
также на диагоналях.
Друзья, вы отлично справились с заданием и, конечно же, убедились, что
магические квадраты не могут быть скучными. Успехов вам в изучении математики!
И до новых встреч!
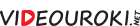
 Получите свидетельство
Получите свидетельство Вход
Вход




 54
54

